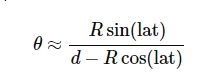Major lunar standstill and moonrise/moonset azimuth fluctuations

The text explains the rare phenomenon, in which the azimuths of moonrise and moonset are more extreme. This situation allows us to see distant landscape features with the lunar disk beyond. Learn more about the lunar standstill and its frequency across the centuries. The changes in moonrise/moonset azimuths can give you a clue of how some Megalithic constructions have been set and how the Moon’s path across the sky would have looked like thousands of years before. Moreover, the declination of the Moon isn’t the same. It changes significantly because of the parallax.
1. WHAT IS THE LUNAR STANDSTILL
If we want to explain what exactly lunar standstill is, we should first know what the lunistice is. Lunistice occurs every 2 weeks when the Moon reaches the farthest point above or below the equator. These points, (called also as lunar geocentric extremes) change their distance to the celestial equator over the lunar nodal precession period of about 18.6 years, when return to the same horizon positions. A lunar standstill is a period when the amplitude of this oscillation at the lunistice is at its minimum or maximum value. It happens once every 9.3 years. When the amplitude is the lowest then the minor lunar standstill occurs. The declination of the Moon during the tropical month for a total range of about 37º. Conversely, when the distance of the Moon to the equator is the biggest, we have a major lunar standstill occurrence with the declination changes up to 57º. The term “lunar standstill” was first used in 1971 in archeoastronomy and describes the lunar equivalent for the “solar standstill” or simply solstice occurring twice a year. Since the solstice describes the extremes in the Sun’s varying declination, the lunistice does the same, but within just the (tropical) month. The lunar standstill phenomenon would have drawn attention in Megalithic times when in some high latitudes the Moon was visible as circumpolar for some time during the 18.6-year cycle (Moon’s arctic circle). It was one of the basics for the development of the prehistoric lunar calendar. The term lunar standstill is used mostly in archaeoastronomical studies, which play around with so-called “horizon” astronomy aimed at near-horizon celestial phenomena.
2. LUNAR ORBIT PERTURBATION
The period of lunar standstill isn’t the same as the period of its solar counterpart. Unlike the solar declination near the solstice, the lunar one keeps changing due to the fluctuation, as you can see in the chart below (Pic. 1).
The mean inclination of the lunar orbit to the ecliptic is 5º08′,7 (Meeus, 1997), although this inclination varies between 5º and 5º18′ (Pic. 2) because the motion of the nodes is not regular.

Pic. 2 Lunar orbit inclination for the example period of 2008-2010 (Espenak, Meeus, 2009/Eclipse.gsfc.nasa.gov)
The biggest lunar orbit inclination occurs when the line of nodes of the lunar orbit is oriented directly to the Sun, which happens at each conjunction of one node with the Sun. It occurs at a mean interval of 173.31 days because this is the average time of the Sun for travel from one node to another and states the equivalent to the interval between the midpoints of two eclipse seasons (Espenak, Meeus, 2009). Indeed, this period is shorter than half a year, because the Moon’s ascending node retrogrades slightly by 3′ 10.62″ daily, making its full 360º route in 18,613 years. In other words, the biggest inclination occurs always around the time when solar and lunar eclipses take place or if the difference between the longitude of the ascending node is 0º or 180º. In the opposite case, when the difference in longitude is either 90º or 270º, then the smallest inclination of 5º occurs.
Now let’s consider this case for the major lunar standstill. The primary condition for a lunar standstill to happen is the location of the ascending node at the right ascension of 0h. In other words, the ascending node must coincide with the vernal equinox (the autumn equinox in the southern hemisphere) – the moment when the Sun enters the northern celestial hemisphere. In a situation such as this, the maximum lunar orbit oscillation will happen only around March and September. This is because the lunar nodes pass the ecliptic roughly at the moment of its passing through the equatorial plane as shown in the graph below (Pic. 3).

Pic. 3 The lunar standstill nodes graphical explanation. When the ascending node crosses the vernal equinox, the lunar orbit inclination has an additive effect to achieve maximum declinations to the north or south of the ecliptic. In the opposite situation, the effect is subtractive (St-and.ac.uk/).
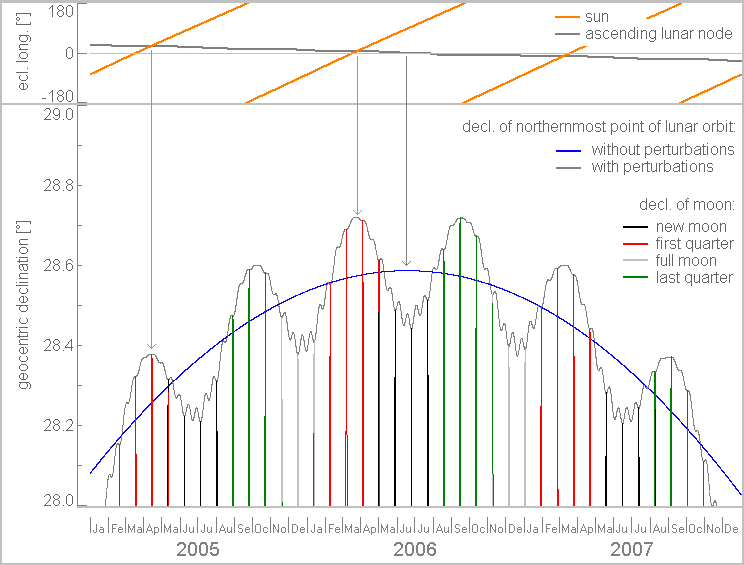
Pic. 4 The graphic representation of major lunar standstill occurrence in 2006 against the lunar orbit oscillation, which looks pretty much the same for all other major lunar standstill periods. The orange arrow shows the maximum lunar orbit oscillation, which marks the eclipse season. The gray arrow indicated the moment when the northernmost lunar orbit would be the biggest without any perturbation. (Archeocosmology.com)
The Sun passes the equatorial plane around March 21 and September 23. If the lunar nodes coincide with this moment, then we have the eclipse season observed around this time. The major lunar standstill occurs at the moment, when the lunar orbit inclination reaches its most extreme point as far as the mean line, without any perturbation concerned. When it happens around a period of minimum lunar orbit oscillation, it produces a subtractive effect decreasing the inclination of the lunar orbit slightly. Conversely, the maximum inclination of lunar orbit happens around March 21 and September 23 at the peak of lunar orbit oscillation, when the absolute lunar declination is the highest. This is why the extremal values of lunar declination are assigned to the phases around the first or last quarter of the Moon whereas the full or new Moon is observed during the minimum lunar oscillation. Practically it means, that an observer is never able to capture the shadow of the Moon during its most extreme declination at its highest point in the sky. This is because the Moon towers around at sunrise or sunset in a geometrical sense. The peak of lunar standstill might occur between two symmetrical perturbations shown above and be unobservable if happens during the new Moon. The moment of lunar standstill doesn’t happen at the same time of the year, which is driven by the discrepancy in time between the nodal precession and the Metonic cycle, which is about 4 months longer. The example above shows the moment of lunar standstill occurring in June 2006 (Pic. 4), which reflects two symmetric peaks of the most extreme Moon’s declination observed both in March and September. In 2025, the analog moment will be observed in January (Pic. 6). There is a common denominator between both, as this moment occurs around the minimum of lunar orbit perturbation. In 1969, for example, the major lunar standstill occurred around April, thereby both charts below feature only one peak with the most extreme declination, which is observed “closer” to the moment of major standstill. Since the maximum lunar orbit oscillation occurs around March and September, it is added up to the extremal absolute value of lunar declination. The absolute value must be stressed because it refers either to negative or positive extreme declination values reached by the Moon in its orbit. As a result, the most extreme values of lunar declination will be observed always around the vernal or (alternatively) autumn equinox.
The major lunar standstill case looks right and it’s rather easily understandable, the minor lunar standstill pattern might bring you a headache. Despite the aim of this text, which isn’t dedicated for the minor one it’s a good occasion to explain it here by the way. First let’s have a look at the pattern below (Pic. 5), in which we can see the monthly geocentric extreme declinations for the Moon for the major lunar standstill of 1969 and the subsequent occurrence of a minor lunar standstill over 9 years later.
The pattern looks different for the minor lunar standstill though. Unlike March or September, the monthly extreme declinations seem to be observed in June or December. During a minor lunar standstill, the ascending node crosses the autumn equinox. It means, that the pattern is somewhat reverted. The maximum lunar orbit oscillation is still observed at the same time (March and September), but it this situation its value is deducted from the extreme absolute value of lunar declination. This is why the lowest absolute values of lunar declination are observed in the spring or autumn period.
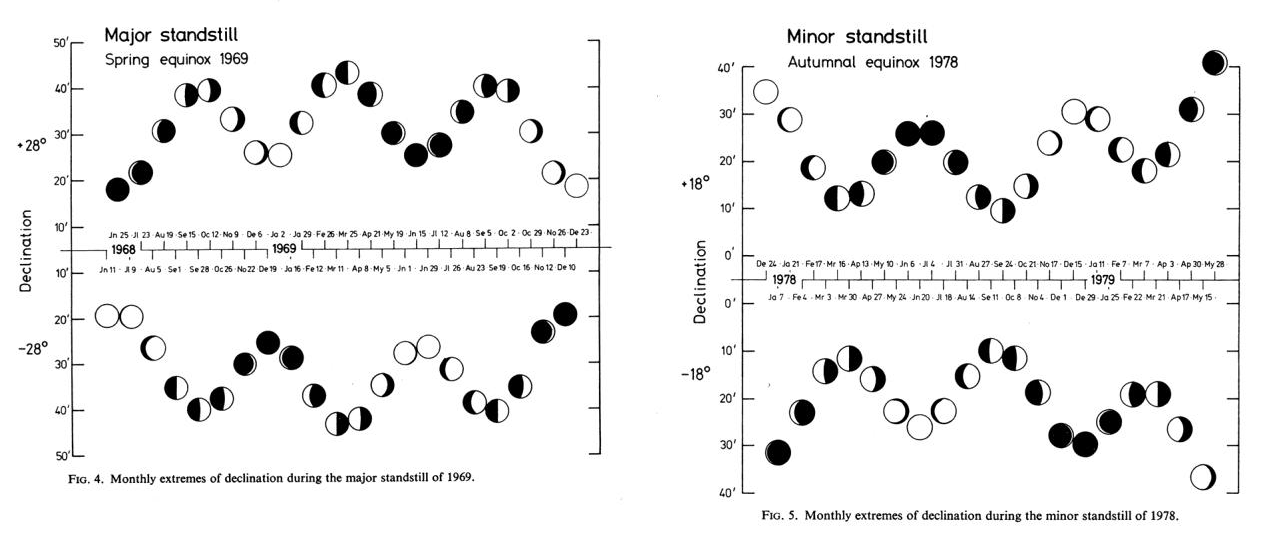
Pic. 5 Monthly geocentric extreme declinations of the 1969 major standstill and the 1978 minor standstill, by date and lunar phase. The major lunar standstill of 1969 was observed around April, and the minor one around July and August 1980. As a consequence, there is only one single peak of most extreme declinations occurring “closer” to these moments – March 1969 and September 1978 accordingly (Morrison, 1980).
The image above (Pic. 5) on the right displays the maximum minor lunar standstill, where the least extreme declination is observed. Unfortunately, the moment, when the greatest minor lunar standstill occurs seems to be marked in some sources incorrectly. By looking for example at the Greatest Annual Lunar Standstills tab, we can find the December-January period indicating the peak of the minor lunar standstill. I guess this is wrong, as the minor lunar standstill marks the moment of the lowest absolute lunar declination possible to achieve for the given lunistice. This particular one will still occur near March or September! The Astropixels.com website decided to point out the most extreme declination for the given year instead. Threading this way, declination such as this occurs always around the moment when the minimum lunar orbit oscillation is observed. In light of gradual changes in the position of lunar nodes, it will be the beginning or end of the given year. Displaying the data like this isn’t quite correct, because the moment of minor lunar standstill indicates the least extreme declination instead.
In the case of a major lunar standstill, these particular matters look much clearer to anyone, as the moment of most extreme declination of the given year indicates the major lunar standstill at once. The best example is the left graph in the image above (Pic. 5) or the pattern below, in which we can see the graphical representation of the current major lunar standstill (Pic. 6).
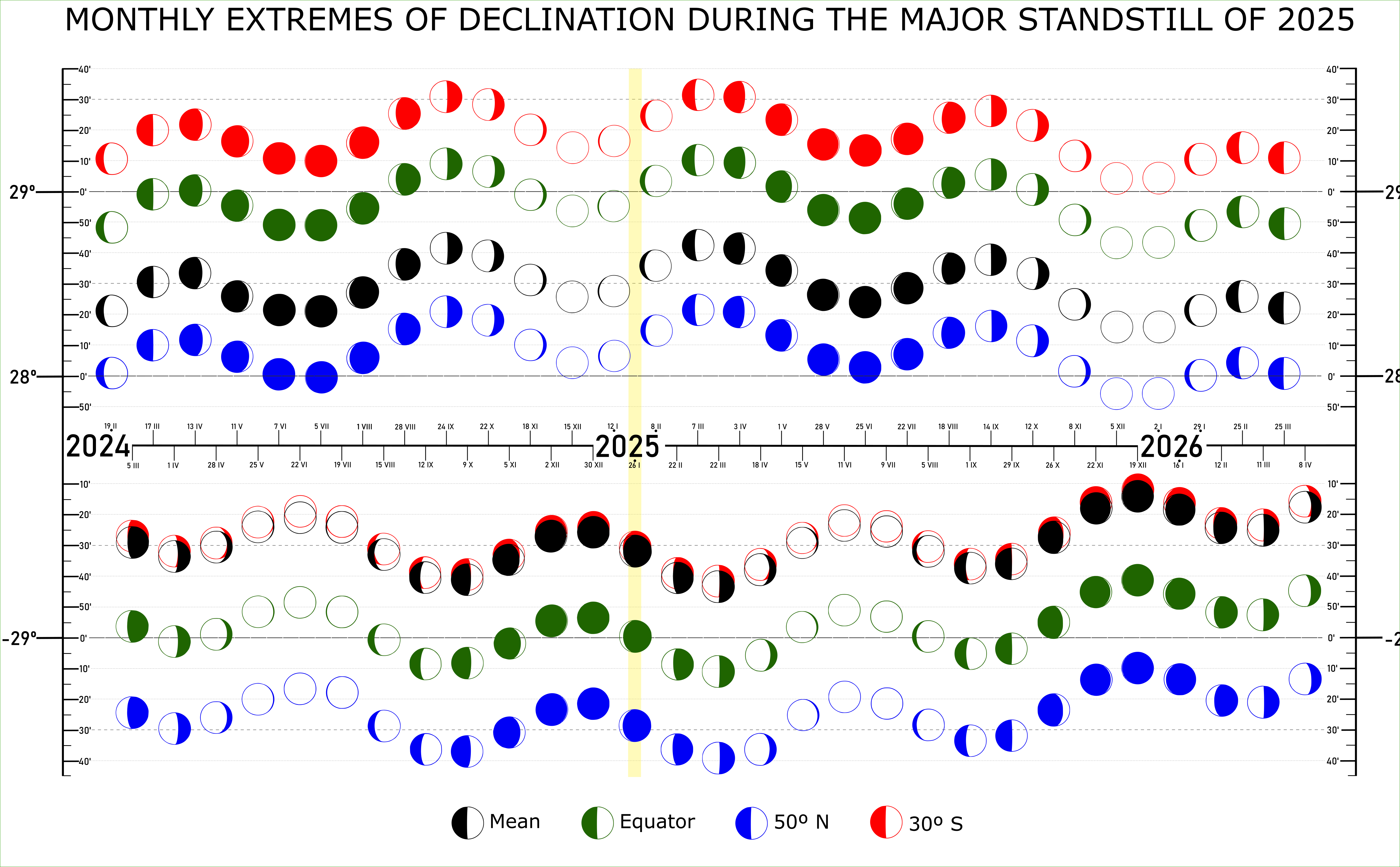
Pic. 6 Monthly extremes of Moon’s declination during the major standstill of 2025 with the breakdown between the latitudes of 50N, equator, and 30S. Ask for the full size here.
Considering the occurrence of maximum lunar orbit perturbation near the vernal or autumn equinox, in practice, the greatest declination will be achieved by the first or last quarter of the Moon, whereas the full/new Moon will fall around the minimum lunar orbit inclination (Pic. 6). The only exception from this rule is the general change of lunar orbit obliquity, which depending on the moment against the major standstill can shift the occurrence of greatest declination by one lunistice period. As a result, the most extreme declination can be sometimes seen in late August-mid October, or late February-mid April.

Pic. 7 The lunar standstill perturbation against the phases of the Moon. The greatest declination of the Moon occurs always at the first and last quarter of the Moon whereas the new or full Moon falls around the minimum of lunar orbit inclination. The red dots mark the “key declinations” for major lunar phases (quarters, new Moon, and full Moon around the major lunar standstill time (Gough, 2018).
 The maximum lunar declination both north and south changes within around 20′ for about a year and it corresponds to the primary 4 lunar phases mentioned in the calendar. Considering the symmetrical shape of the major lunar standstill, as occurred in June 2006 we shall see the lunar limb position changes within less than 1 angular degree. However, this situation applies only for standstill culminating during the peak of minimum lunar orbit perturbation i.e. in June or December. In practice, a situation such as this might happen once for a tenth standstill, so every 186 years considering just one type of standstill. The span of 44-142 years applies to any standstill. In doesn’t change the fact, that in the vast majority of cases, the lunar band during the standstill period exceeds 1º and most extreme declination is observed only once.
The maximum lunar declination both north and south changes within around 20′ for about a year and it corresponds to the primary 4 lunar phases mentioned in the calendar. Considering the symmetrical shape of the major lunar standstill, as occurred in June 2006 we shall see the lunar limb position changes within less than 1 angular degree. However, this situation applies only for standstill culminating during the peak of minimum lunar orbit perturbation i.e. in June or December. In practice, a situation such as this might happen once for a tenth standstill, so every 186 years considering just one type of standstill. The span of 44-142 years applies to any standstill. In doesn’t change the fact, that in the vast majority of cases, the lunar band during the standstill period exceeds 1º and most extreme declination is observed only once.
The Astropixels tab shows the greatest annual lunar declination possible to occur, which mostly happens in the December-January period, thereby worth attention if the table below shows the minor lunar standstill dates for the current century (Tab. 1).
Tab. 1 The dates of minor lunar standstill over the XXIst century, which correspond to the maximum lunar orbit oscillation. Because the minor lunar standstill is a result of coincidence of lunar node with the autunm equinox,the absolute declination decreases by lunar orbit inclination.As a consequence the minor lunar standstill represents the closest declination numbers tothe ecliptic. The emboldened values refer to the closest maximum lunar orbit oscillationto the moment, when the minor lunar standstill is observed around the single lunistice time (marked red).
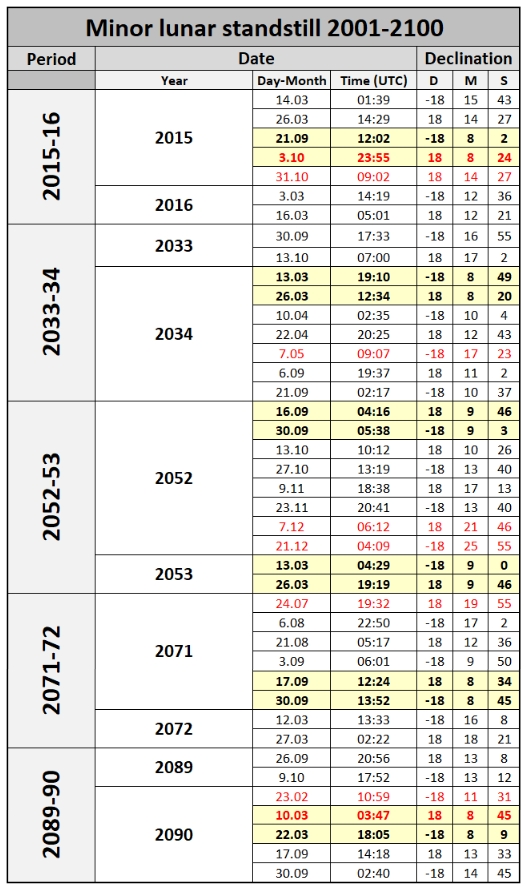
In this tab you can see what certain dates should be considered as closest to the minor lunar standstill, the last minor lunar standstill occurred in October 2015, the next one will be on May 2034, and another one around December 2053, on July 2071, and the last one on early March 2090.
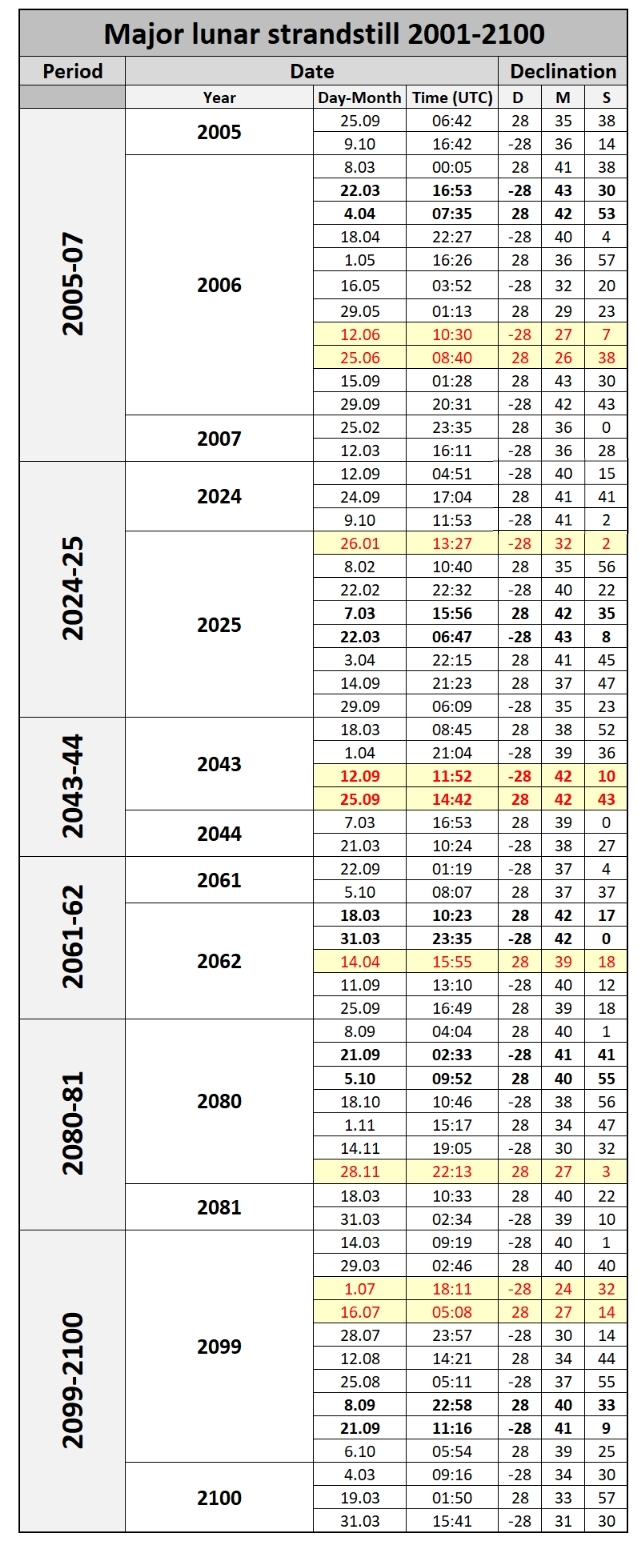
By returning to the major concern of this text – the major lunar standstill let’s see the table below, which presents the major lunar standstill periods in the XXIst century (Tab. 2) including the most extreme declinations.
Tab. 2 The dates of major lunar standstill over the XXIst century, which correspond to the maximum lunar orbit oscillation. The emboldened values refer to the closest maximum lunar orbit oscillation to the moment, when the minor lunar standstill is observed around the single lunistice time (marked red).
3. LUNAR STANDSTILL VS HORIZON RANGE
Apart from the perturbation superimposed on the 18,6 years cycle of nodal precession, it’s fairly legitimate to mention the rapid changes of lunar declination within one lunation. The period, in which the Moon is above the horizon, especially at positive declination will be eventually subject to slight changes in lunar declination. As the Moon revolves around Earth within about 29,5 days as far as the synodic month is considered we shall expect the utter lack of symmetry between the azimuth of moonrise and moonset. This particular phenomenon is best visible during the major lunar standstill when the lunar declination changes so fast. In practice, it means, that the most extreme azimuth of moonrise or moonset will apply just for specific longitude rather than the entire globe. It is assumed, that the declination deficiency within 12 hours might be even larger than the perturbation caused by the lunar orbit inclination (Thom, 1971). Moreover, even the declination of the Moon during its mid-transit across the sky will be different than when it rises or sets from a certain location. The disjunction between the moonrise and moonset can be 3,9′ (Sims, 2019) considering the moment of most extreme declination at mid-transit.
The table below (Tab 3) shows the local circumstances for moonrise and moonset during the forthcoming major lunar standstill in 2025. All the moonrise/moonset ephemeris can be calculated from this simple formula (F1).
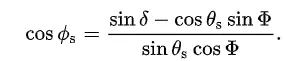 In Excel, you should prepare your values by calculating the sinus and cosinus for them, as shown below.
In Excel, you should prepare your values by calculating the sinus and cosinus for them, as shown below.
=SIN(Φ*PI()/180) =COS(Φ*PI()/180)
Your Θ is the zenith angle, calculated from the zenith to the height, at which the Moon is situated. We consider the rough moonrise/moonset azimuth indicating the moment of the Ist or IVth contact we should be aware of the mean astronomical refraction value around 35′ at the horizon. In the case of the moment, when the Moon’s upper limb appears or disappears beyond the horizon, the Moon’s angular size must be considered. The angular diameter of the Moon can be calculated from the formula presented below (F2):
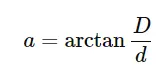 where in Excel it looks like this:
where in Excel it looks like this:
a=ATAN(D/d)*180/PI()
and calculates the angular size of the Moon’s diameter straight away. The distance to the Moon on a given date can be obtained from this link. To know the lunar angular diameter, we need to add the Moon’s angular radius to the refraction value. It should give us something around 50′, which must be added to the zenith angle later on. The final value of the zenith angle will be the 90°+ value obtained from the sum of the refraction value (r) and angular size of the lunar radius (a).
In Excel it could look like this (F3):
Θ = 90+((a/2)+r)
By having all the values prepared upon the formula F1 we can use the following Excel formula:
=DEGREES(ACOS((BL4-(BM3*BL2))/(BL3*BM2)))
where the following cells correspond to the values in the formula F1.
The value we receive applies to the azimuth of moonrise. Threading this way, this value is added to the north azimuth of 0º. If we want to get the azimuth of moonset, we need to subtract the same value from the final azimuth of 360º. Next, optionally we can convert these decimal values to the DMS format, which this article has already explained.
The results presented in the Table below (Tab. 3) show not only the comparison of moonrise/moonset azimuths during the extreme lunar declinations around the 2025 lunar standstill. The table also shows the correctness between the extreme Moon’s declination and the example of some latitudes considered.
Tab. 3 The difference in azimuth of moonrise/moonset between the angle based on extreme declination and angle observed at the given moment against the moment of extreme declination.
The aforementioned changes in declination within just one “lunar day” lead to the conclusion, that the moment of moonrise or moonset doesn’t need to coincide with the moment of greatest lunar declination. The apparent azimuth standstill limit will be different both concerning the given longitude as well as the moment of lunar orbit perturbation.
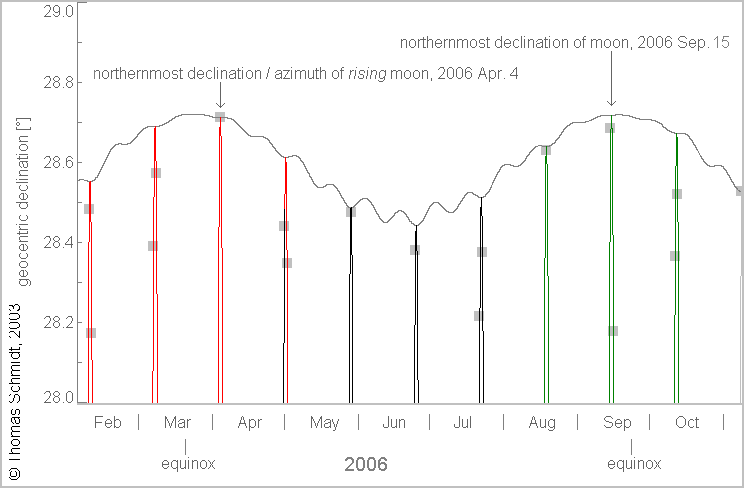
Pic. 8 The difference between the most extreme azimuth of moonrise/moonset against the most extreme lunar declination. The moonrise/moonset events are marked by the gray box (Schmidt, 2003/Archeocosmology.org).
The table above (Tab. 3) shows it clearly. Let’s look at the time when the most extreme Moon’s declination is to be observed. This time isn’t suitable for the time of moonrise/moonset at the local meridian. If it happens this way, the observer won’t be able to see the moonrise or moonset at the azimuth based on the moment of the extreme declination. He will do so only when this moment coincides roughly with the time of moonrise or moonset. By looking at the table (Tab. 3) we can point out 2 examples almost such as this, which are marked red. In these cases, the moonrise occurs shortly after the extreme declination of the Moon is observed. As a result, the discrepancy between the geometrical azimuth and true azimuth is smallish. On the other hand, the moonset for these 2 locations will feature the most significant difference in azimuths, as the phenomenon occurs several hours after the Moon’s declination reaches extreme value. The chart on the right shows the graphical representation of the problem (Pic. 8).
The circumstances of the Moon based on the moment of extreme declination look quite complicated (Pic. 9). Like it was flagged up the lunar declination changes fast enough, that’s why its changes are noticeable within the given “lunar day”.
Case I – represents the situation, when the major lunar standstill extreme declination (a) coincides with the moonrise. Then as the Moon goes up in the sky its declination decreases reaching a half value about the lunar noon (b) and the full decrement value (c) of approximately 11,6′ at the moonset.
Case II – shows the situation, when the most extreme declination is reached around Moon’s culmination. The observer can see the Moon towering extremely high above the horizon, but its rise/set azimuths are shifted as the declination decreases by about 3,9′ (b and b’).
Case III – in this case the lowest declination is observed at moonrise, which rises gradually over the day, reducing the total decrement by half (b) around the lunar noon and finally the most extreme value (c) at moonset.
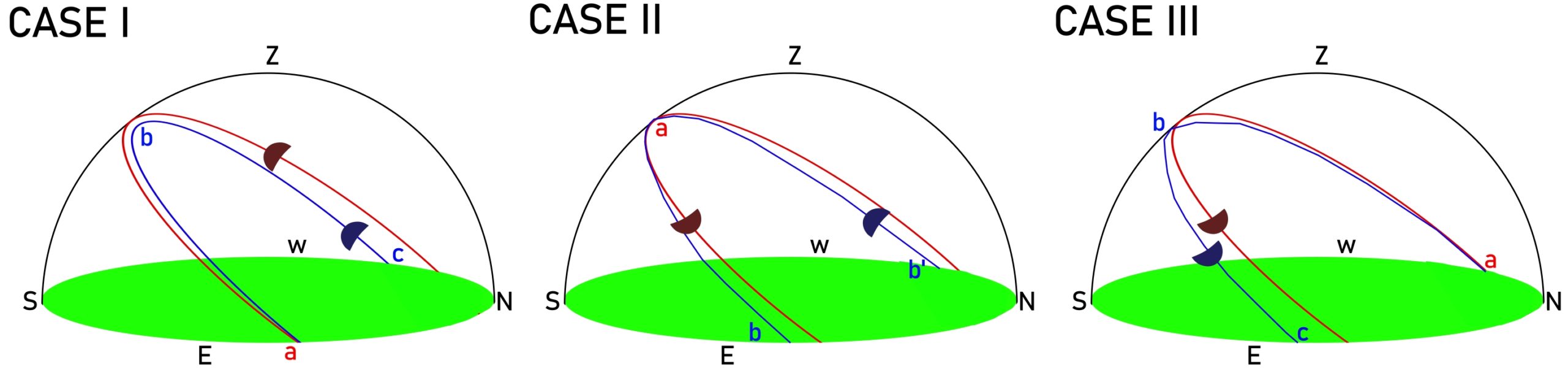
Pic. 9 The circumstances of the Moon above the horizon based on the moment of extreme north declination where the red path corresponds to the extreme declination and the blue path to the changes against the extreme moment, where: a – the moment of true extreme declination; b & b’ – the half deficiency of declination; c – full deficiency of declination.
The table below (Tab. 4) shows how the lunar declination changes by longitude. There are 4 places separated by 1° from each other and each of them features a different Moon’s declination at its culmination, which occurs consistently every 4 minutes in a sequence of consecutive places.
Tab. 4 The 4 places in Poland are located at latitudes of 50º North, separated by 1º of longitude between each other, effectively giving a 4-minute difference in culmination. Even at short distances like these, the change in the Moon's declination is noticeable.
The other matter is the Moon’s phase during the event. The most extreme moonrise/moonset azimuth possible to reach doesn’t guarantee successful observation. It might happen, that the Moon, indeed will make the Ist or IVth contact with its darker side. Let’s understand it in the example shown below (Pic. 9,10).
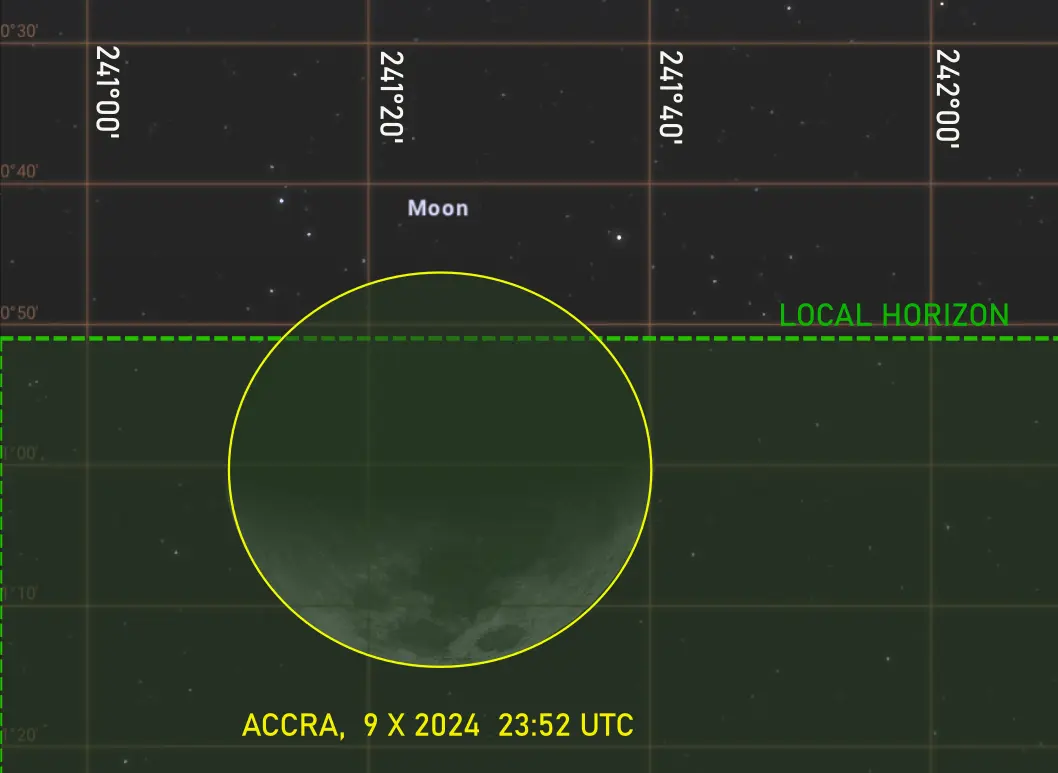
Pic. 9-10 The example of moonrise and moonset in Accra at the moment of most extreme Moon’s declination observed. Despite theoretical visibility of the Moon’s limb above the horizon at a given azimuth, the object won’t be detectable. The image above shows the first quarter moonset on October 9, 2024. The image below represents an opposite situation around 2 weeks earlier (based on Stellarium-web.org). Even if the Moon reaches its most extreme azimuth when rising or setting near the major lunar standstill, it might remain invisible to the observer, especially since the most extreme declinations are observed around the quarters. A situation such as this will be applicable mainly to low latitudes (Stellarium-web.org).
The same thing applies to the most extreme altitude of the Moon above the horizon, which can be seen only from the meridian at which the Moon is currently towering. Assuming, that the most extreme lunar declination is achieved at midnight, 12 hours later it will decrease by about 11,6′ (Thom, 1971). In practice, the Moon can be observed as high in the sky as possible, but its rise/set azimuths won’t be extreme. We shall assume, that these described extrema are presumed to be observed about once an exeligmos from the specified location.
Another issue to be covered here is the general decrement of the extreme lunar declinations. The reason behind this is the change in Earth’s axial tilt (Milankowich cycle), which directly affects the obliquity of the ecliptic. Currently, the Earth’s axial tilt is 23°26′21.406″ as per the Astronomical Almanac in 2010. It wasn’t always like this, as you can see in the graph below (Pic. 11).
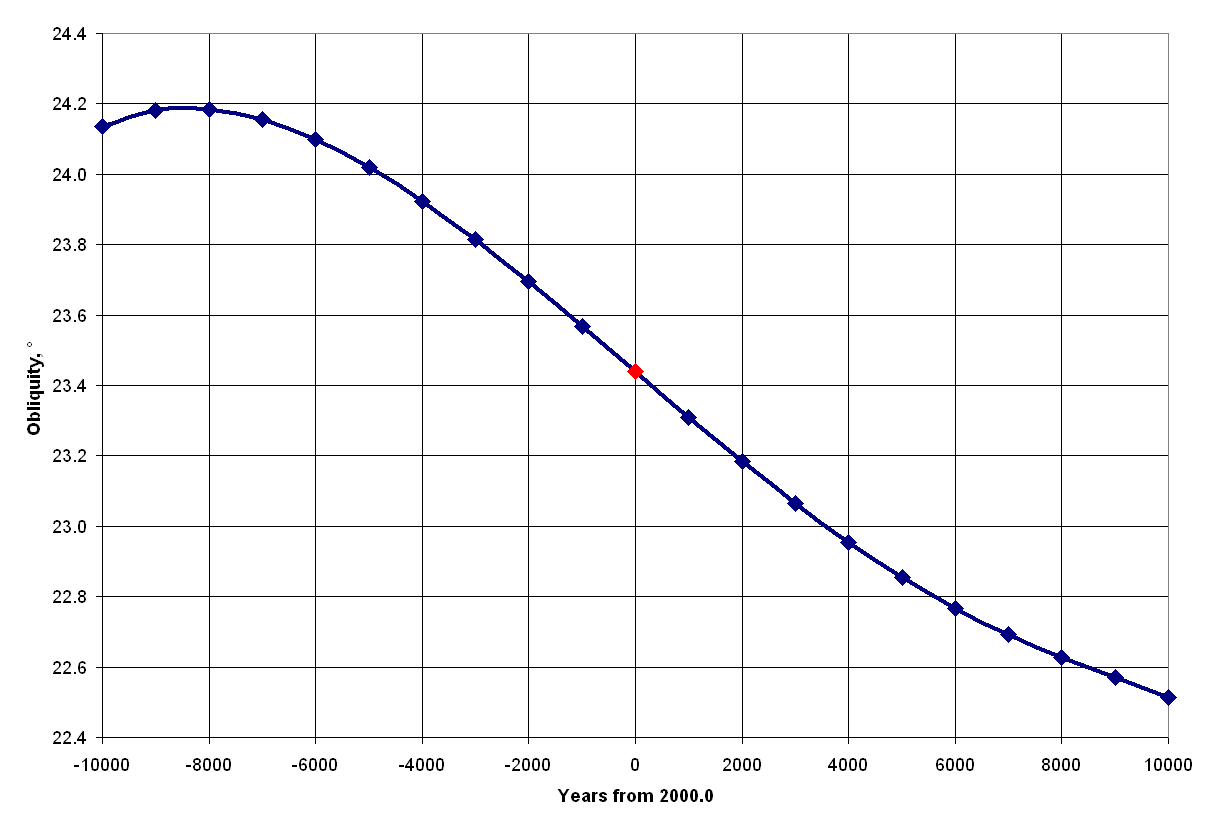
Pic. 11 The obliquity of the ecliptic changes through 20000 years (Laskar, 1986).
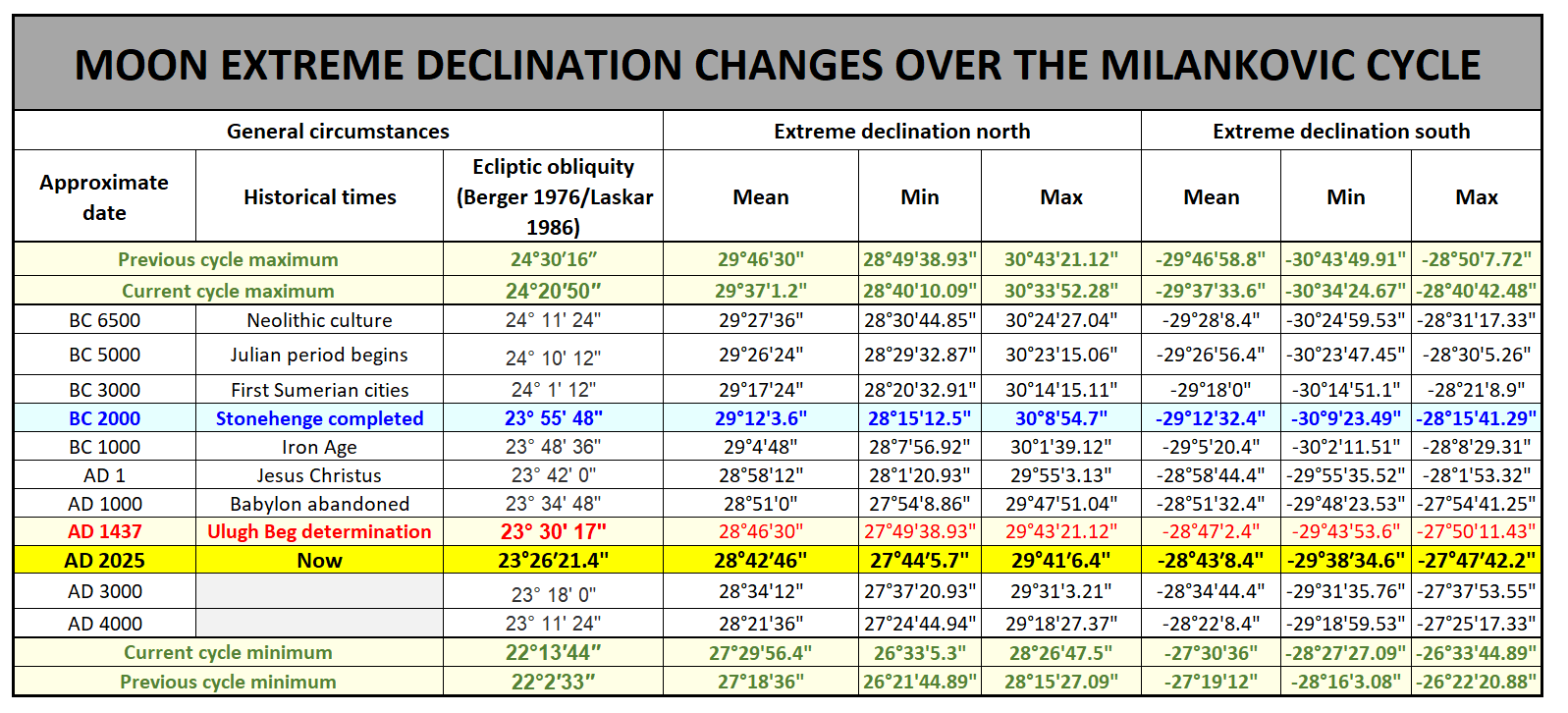
By knowing the current obliquity of Earth’s orbit, we can have the most extreme declination of 28º42’36” as expected on March 7, 2025, as well as -28º43’8″ on March 22. As far as the mean distance to the Moon is concerned these results will range accordingly from 27º45”45″ (March 7) to -29º13’20” (March 22). The table below compares these values over random moments in history bringing some information about extreme declination changes in major lunar standstill circumstances considering the same circumstances as estimated in March 2025 (Tab. 5).
Tab. 5 Changes of lunar declination over the Milankovich cycle concerning extremes of Earth's ecliptic obliquity are estimated in former cycles. The table presents the approximate Moon's declination around some notable historical time (based on. Berger, 1976 and Laskar, 1986).
There is a discrepancy between these 2 sources of Earth’s ecliptic obliquity changes. According to the chart above (Pic. 5) the maximum obliquity should have been reached about 8500 years ago with the maximum of approximately 24º11’24”. The other source (Berger, 1976) provides the obliquity value of 24º20’50”. In practice, we would have as large an uncertainty as half of the difference between the minimum and maximum lunar orbit perturbation. It’s enough to notice the potential changes in the azimuth of moonrise/moonset. For the sake of simplification, the chart above has been considered for further analysis. The other ambiguity can be found in the first official Earth’s orbit inclination value obtained by Ulugh Beg, who computed it to the value of 23º30’17”. Considering the extreme lunar declination during the major lunar standstill we can obtain the value of about 28°47′, which seems to be too low compared to the table below presenting the most extreme lunar declinations between 1501 and 2500 years, computed by Fred Espenak (Astropixels.com) (Tab 6). We can find there are more extreme declinations observed around 100 years later. Regardless of this unclarity, which will be resolved in the future, we can see how these values change across the millennia and how our ancestors and prehistoric inhabitants could see them. At first glance, we can see, that at the time when Stonehenge was completed the difference in solstices and then lunar declinations was about the diameter of these two bodies.
Tab. 6 The most extreme declinations of the Moon at greatest major lunar standstills over 1000 years between AD1501-AD2500 (Astropixels.com).
The table above (Tab. 6) leads to the initial conclusion, that we are living in the times when the absolute extreme declination of the Moon decreases by about 8′ per 1000 years. It’s fairly a lot considering the average angular size of the Moon, which is just about 4x larger. This is just for now because as the chart above (Pic. 11) shows, it will slow down in later millennia. Anyhow in this time, we shall expect, that the obliquity of the ecliptic decreases by about the size of a solar/lunar disk per 4000 years or so. These changes are fast and indeed, can be noticeable even within the century. In practice, they have an impact on the subsequent major lunar standstill (Pic. 12).

Pic. 12 The decreasing extremes of lunar declination between 1900 and 2100 are caused by decreasing obliquity of the ecliptic at the same time (Meeus, 1997).
The nutation also impacts the extremes of lunar declination but to a lesser degree. Nowadays, we shall expect, that every consecutive major luinar standstill will result in an overall declination deficiency of about 5″ on average. In a practical sense, the occasion of seeing the lunar disk grazing some thin artificial object from the given location might be the last one for centuries! We can see, that these changes aren’t uniform and occur in stages. This is driven by a distance of major lunar standstill occurrence against the vernal equinox. Worth mentioning here are the megalithic constructions based on lunar declination extremes in ancient times, which were fairly quite different than nowadays. It was computed, that for the last 4000 years, the extreme declination of solstices decreased by about 27′, assuming that the rate of change of the obliquity of the ecliptic is about 0.7′ per century (Gough, 2014). In other words, all the putative precision alignments based upon the historic observation are somewhat not possible to confirm nowadays due to the aforementioned reason. The pattern below shows pretty much how the problem looks like (Pic. 13).

Pic. 13 The lowest point reached by the Moon as seen from the Saxa Vord 284m.a.s.l [60° 49′ 34.56″ N] during the current major lunar standstill with comparison to the events in former centuries and assumption of the same timespan against the moment of most extreme declination. Because of its elevated position, the Moon could have been visible as a result of a horizon dip. A thick line marks the horizon line (based on Laskar, 1986 and Peakfinder.org).
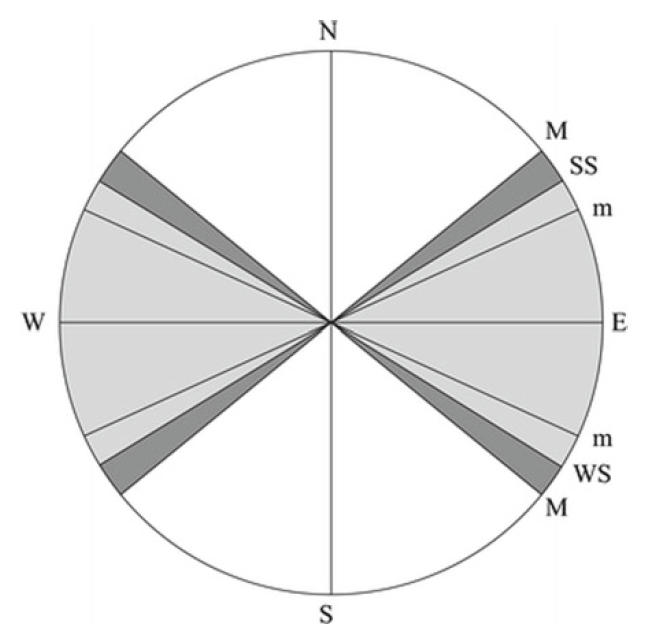
Pic. 14 The lunar standstill moonrise/moonset azimuth vs sunrise/sunset azimuth at solstices, where: N,E,S,W – major directions; M – major lunar standstill azimuth range; SS – summer solstice azimuth range; m – minor lunar standstill azimuth range; WS – winter solstice azimuth range (Magli, 2016).
There is around a 48′ angular difference between the ecliptic obliquity observed today and over 8000 years ago including approximately 37′ since megalithic times. A situation such as this has an impact on the azimuths of extreme moonrises and moonsets and especially on the size of the Moon’s arctic circle. The example above (Pic. 13) shows, that it would have been possible to see the Moon circumpolar from northern Shetlands (Thom, 1971), specifically at elevated grounds, which results in a horizon dip. Concerning analogic changes observed at moonrise or moonset azimuths the example in chapter 6 (Pic. 26) explains it well. A correction such as this should apply to all Megalithic constructions located worldwide, in which certain elements have been based exactly on extreme azimuths of moonrise and moonset at the time when they were built.
The most known challenge applies to Stonehenge – one of the world’s biggest megalithic structures located in Wiltshire, UK. It is speculated that the major lunar standstill extreme azimuths for the monument’s design and purpose. No one has systematically observed and recorded the phenomenon at Stonege, so the correlation between certain stones and major lunar standstill isn’t known well enough. The research is going to be undertaken during the forthcoming 2024-2025 major lunar standstill which is to be associated not only with the construction but also with the ancient people, who probably were aware of the major luinar standstill. There are quite a lot of places like this across the UK and in other parts of the world.
The primary concern of the major lunar standstill is the maximum monthly range of moonrise and moonset, which is beyond the range, that the Sun reaches at solstices. This is presented well in the image below, which includes the lunar standstill azimuth relation to the solstices (Pic. 14).
During the major lunar standstill, the moonrise and moonset reach their farthest apart points along the horizon, unusually far north and south. It happens every 13 days within the year on average. The Moon behaves as if it were a “super-Sun” (Sims, 2016). Conversely, the minor lunar standstill provides no horizon interests.
4. THE INFLUENCE OF REFRACTION ON HORIZONTAL LUNAR ALIGNMENTS
Both astronomical and terrestrial refraction as well as the lunar parallax described below are phenomena, that require some corrections and adjustments to the original Moon’s geocentric extremes to then translate the horizon properties of lunar standstill (Lionel, 2006). At 5º above the horizon, the refraction error to altitude amounts to 10′. At the horizon, this value increases to 35′. Depending on the meteorological conditions, like the temperature inversions and pressure the refraction effect will be higher especially near the horizon and also in low-altitude locations. In conclusion, we should expect significant refraction deviations at altitudes below 1 degree particularly so for negative altitudes (Gough, 2018). Deviations in refraction lead to errors in calculated declinations with corresponding errors in azimuth on the horizon (Sampson, 2000). The problem is significant because of the variations in atmospheric conditions the apparent declination of an observed low-altitude object can be altered by at least several arc minutes, and possibly by as much as half a degree (Schaefer, Liller, 1990). The best example can be seen in the image below, which includes over 100 observations made in Scotland, typical for low-temperature gradients (Pic. 15).
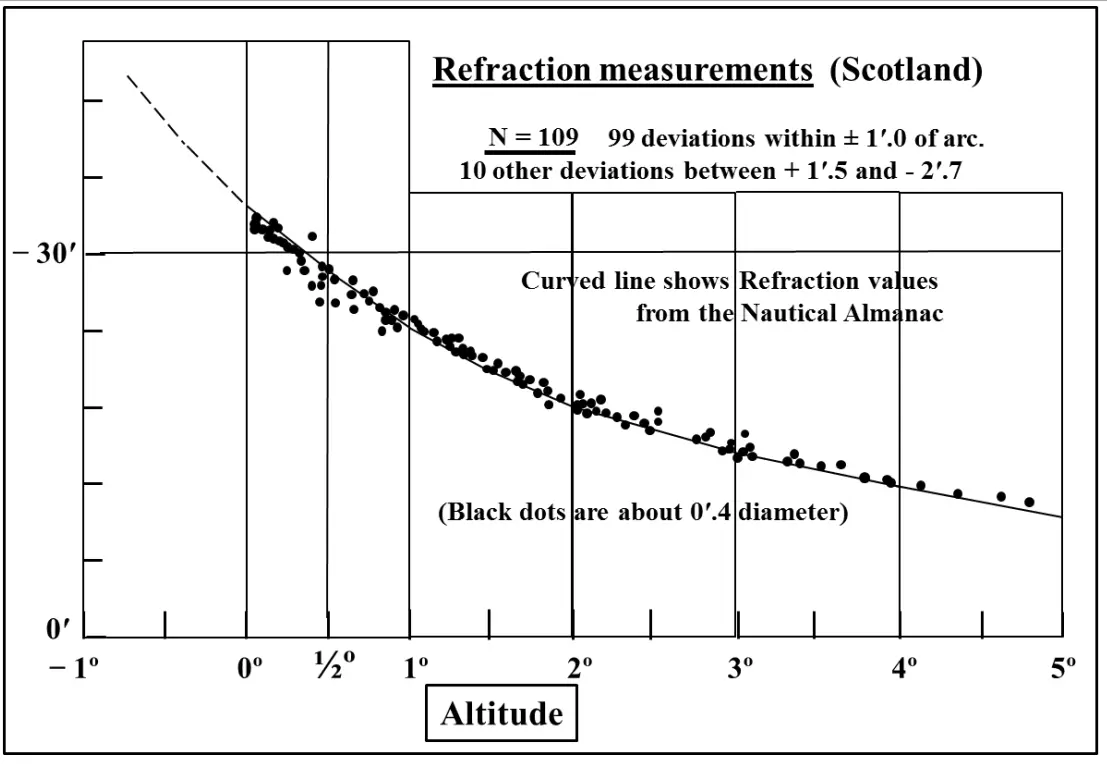
Pic. 15 The refraction measurements in Scotland, where the curve represents the higher influence of the refraction as the celestial body is lower above (or even below) the horizon (Gough, 2018).
However, the example above doesn’t cover the highest values of refraction possible to obtain during temperature inversions, which are quite rare in that area. The temperature gradient can cause changes in refraction values at low altitudes (Schaefer,Liller, 1990). Other large refraction deviations are observed from high-elevation sites, where the dip of the horizon is observed. For example, the standard deviation from Mauna Kea is 16.2′ of arc comparing 3′ of arc for an altitude of 120m (McCluskey, 2017). The refraction measurements are essential for making precise lunar alignments, the same as presented in the image below (Pic. 16).

Pic. 16 Precise lunar alignments at Fort, Argyll, Scotland, UK during the extreme north declination at major lunar standstill.
These precise lunar alignments should be done in the case when we have some suitable horizon features in the vicinity. This is a matter of terrestrial refraction, which reflects the horizontal ray between two points on the ground. It features unpredictable variations being affected by the weather, wind, time of the day, and local terrain. The weather elements apart from those mentioned above can include also the wind and cloud presence. The lowest terrestrial refraction is estimated to be observed in the early afternoon, whereas the highest is after sunset. As night approaches, the ground cools by radiation to a clear sky making cold air layers located at the lowest. As a consequence, the normal fall of air density with height is enhanced increasing the density gradient, which bends the light ray and enhances the refraction. Assuming, that both objects lie within the same air properties, the effect of refraction is proportional to the distance between them.
5. THE INFLUENCE OF LUNAR PARALLAX ON ABSOLUTE MAXIMUM POSITIONS
Because the Earth is a large body, we should be aware, that the position of the observer on the Earth affects the direction in which he sees the Moon (Thom, 1971). The basic influence of lunar parallax can be expressed by the asymmetry in the apparent lunar declination observed in the sky during extreme moments. The Moon observed from the southern hemisphere seems to have a higher apparent declination. This situation has an impact on the maximum altitude of the Moon above the horizon from the given location. In fact, during the standstill the Moon’s geocentric extremes occur during its mid-transit, not when the Moon meets the horizon. The parallax correction must be always made to adjust for observation from a specified position on the surface of the earth (Lionel, 2006). Let’s consider the image below (Pic. 17) which displays the geometrical essence of lunar parallax.

Pic. 17 The geometrical representation of lunar parallax, where: R – the distance between 2 points on Earth with respect to the Earth’s polar radius; d – Earth-Moon distance.
At a pole-to-pole distance, the lunar parallax is approximately 1° 53′ 39.5″ taking into account the mean distance of 384400km between the Moon and Earth. It will vary accordingly as it is shown in the table below (Tab. 7).
Tab. 7 The major lunar standstill, the circumstances of lunar declination against the parallax, and the moment of apogee/perigee. The 2024-2025 period is considered the best example of coincidence with perigee/apogee to occur later in the XXI century.
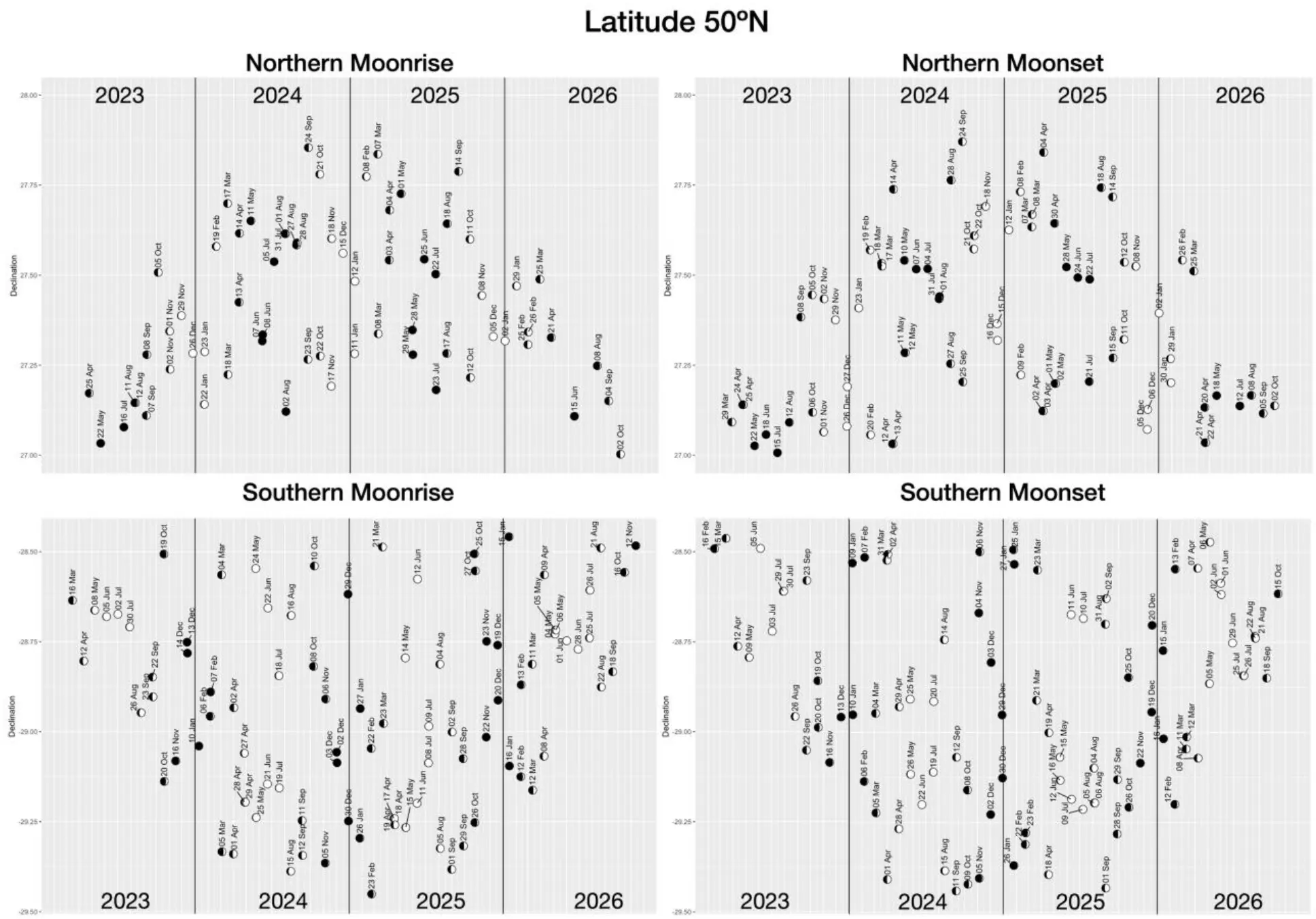
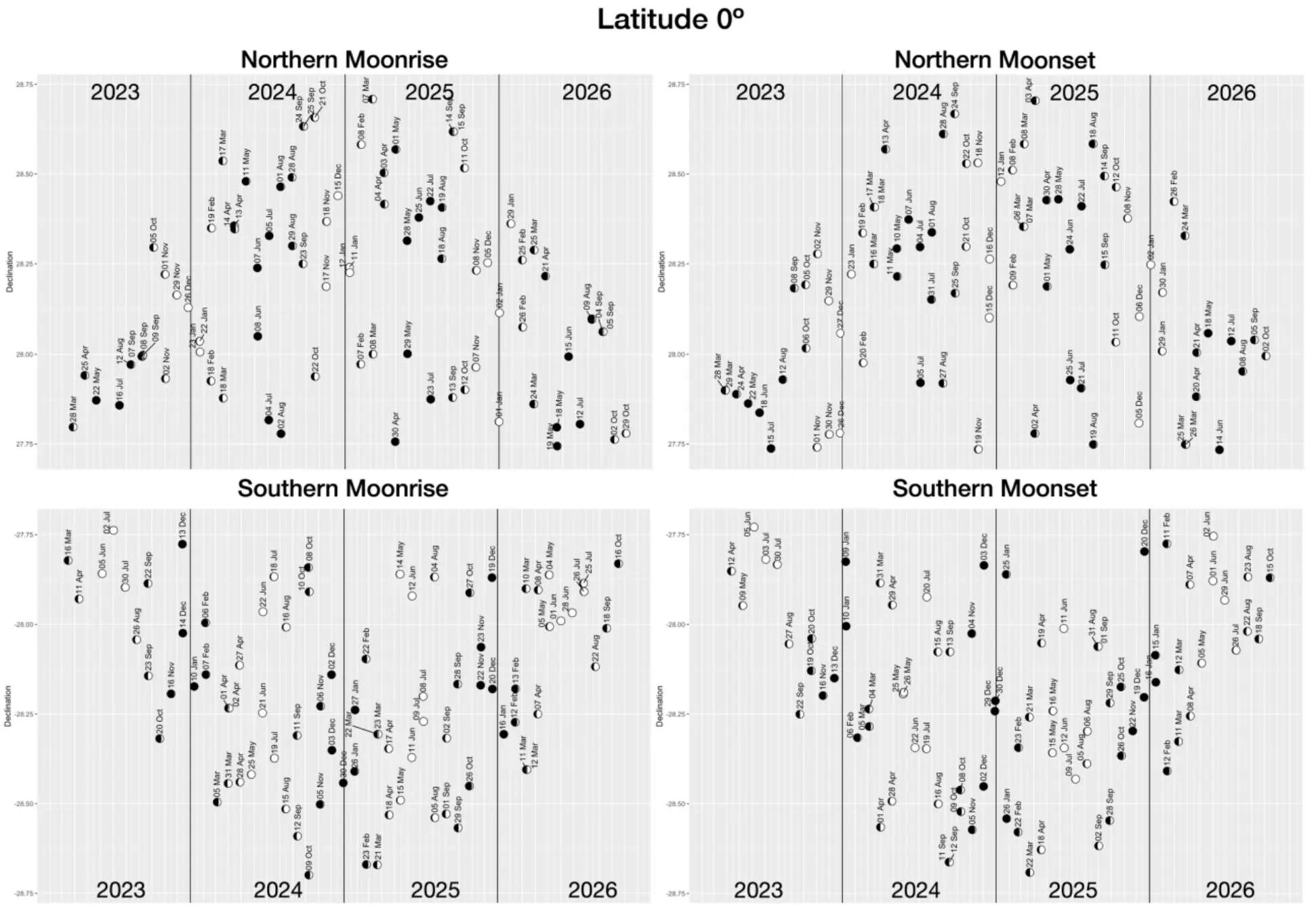
Eventually, the extreme declinations of the Moon are estimated to be observed at the latitude, where the Moon passes the zenith. When we move north or south this declination will change as seen in the images below (Pic. 9-11). However, they should be approached with a distance as the mean declination has been computed from the equator. For better reference, we should look at the graph at the beginning of this text, where the declination of the Moon during the extreme standstill south shows almost no difference between the latitude of 30ºS (Pic. 5).
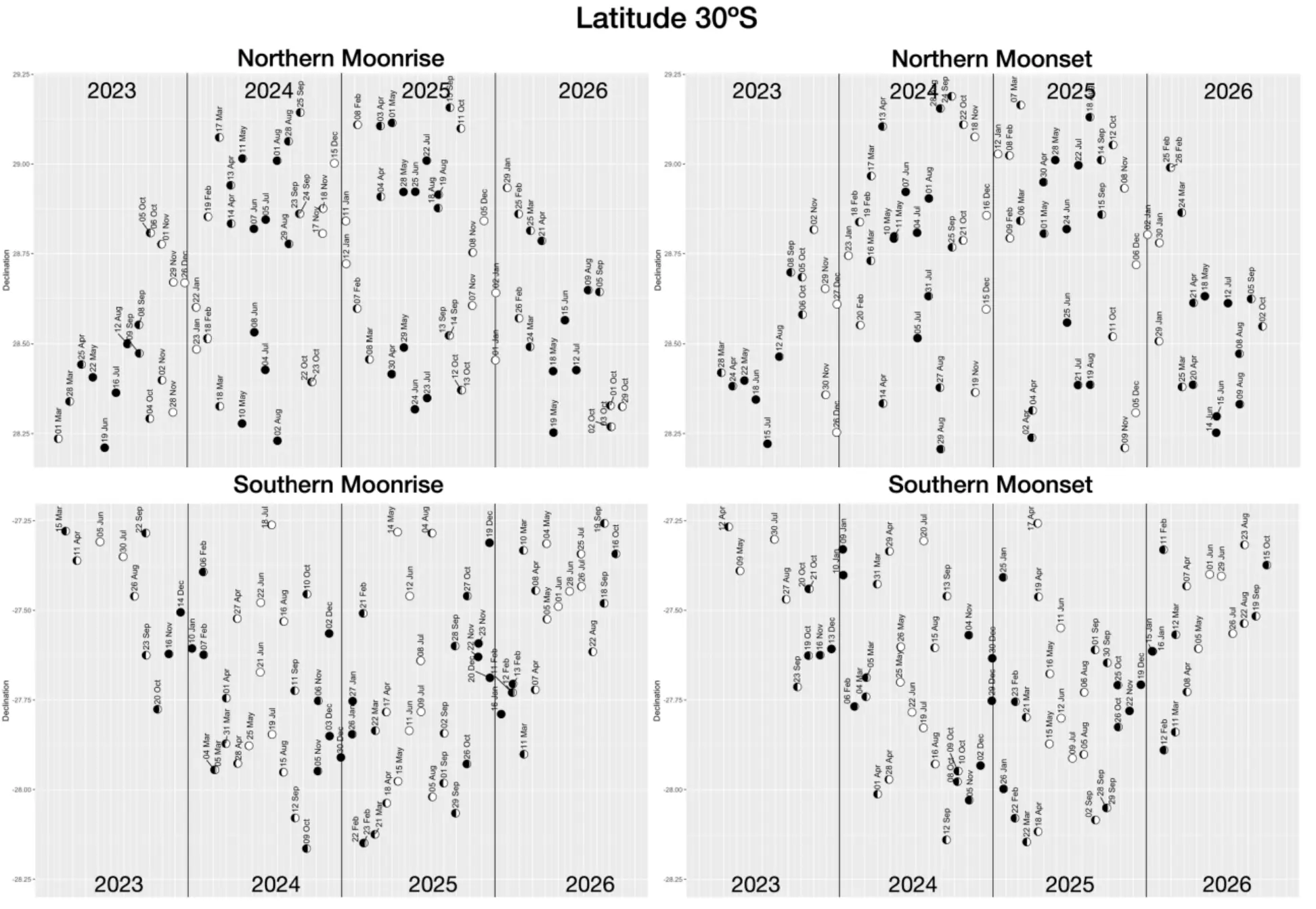
Pic. 18-20 The southern and northern 2023-2026 major lunar standstill circumstances for the latitudes of 50N, 0, and 30S respectively. Despite using the equator as the reference point you can see the difference in the Moon’s declination, which is driven by lunar parallax (Ellingson, Silva, 2024).
The lunar parallax will be noticeable at smaller distances. If we want to calculate it exactly, at least 2 additional formulae would be needed. The first one will play with a distance between one latitude and another as below (F4):
where:
R – Earth’s polar radius
d – Earth-Moon distance
lat – latitude
In Excel, our formula should look as follows:
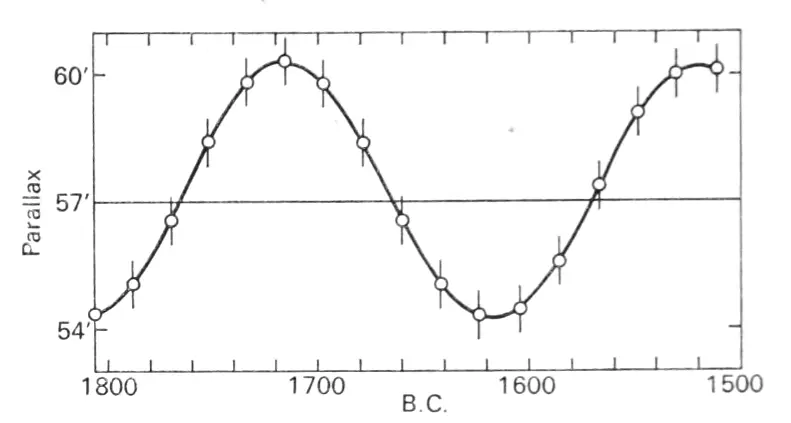
Pic. 21 Moon’s parallax at the north declination maxima at the major standstill from 1800 to 1500 BC (Thom, 1971).
p1=R*(SIN(lat*PI()/180))
next:
p2=d-R*(COS(lat*PI()/180))
and finally:
p = DEGREES(p1/p2)
should give us a result of parallax in degrees from the latitude, at which the Moon can be seen in zenith.
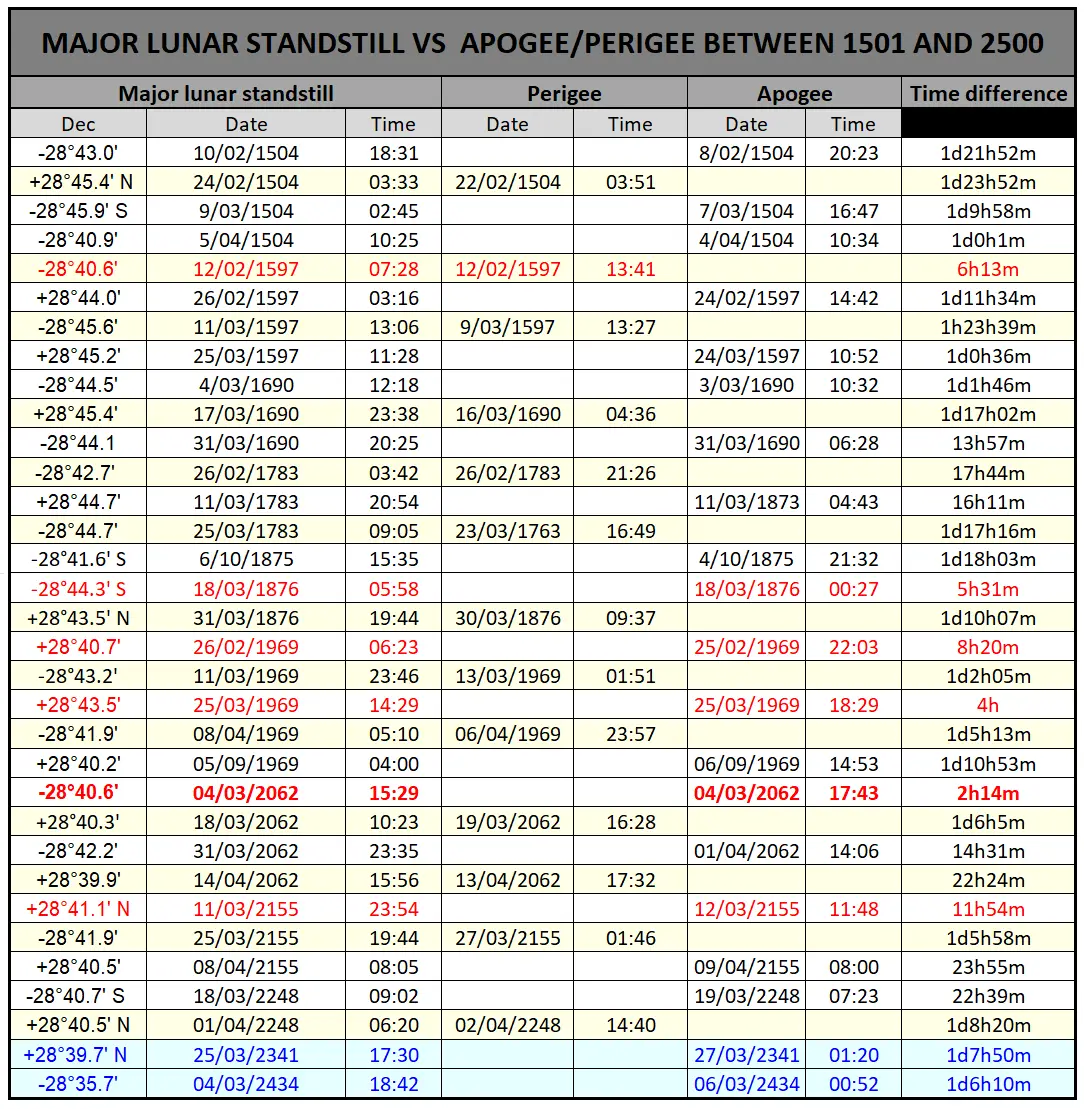
You need to repeat this calculation for another latitude to check the parallax between the two of them. The biggest lunar parallax is observed when the Moon is on the horizon (horizontal parallax). The horizontal parallax is inversely proportional to the distance to the Moon. When the distance is the lowest (at perigee), the parallax is the greatest reaching 61,5′ whereas at apogee it can be about 53,9′. The mean value concerning the time is 57’3″ (Thom, 1971). This is the value measured from the latitude at which the Moon passes zenith to the latitude at which the Moon’s upper limb grazes the horizon. The pole-to-pole parallax is doubled. The chart above shows exactly how often the most extreme Moon’s declination coincides with the moment of apogee (Pic. 21). It’s unlikely to be less than 93 years (Thom, 1971). The table above (Tab. 7) shows when it happens in the current century. The largest parallax is to be observed in 2062 when the major lunar standstill is quite well synchronized with perigee/apogee times. Previously we had a situation such as this in 1969. The tab below (Tab. 8) displays more dates over the 1000 years (1501-2500).
Tab. 8 The major lunar standstill occurrence against the moments of perigee/apogee included extreme absolute declinations higher than 28°40' less than 48h to the perigee or apogee over 1000 years between 1501 and 2500. Because of the decrement of Moon's extreme declination discussed earlier in XXV century the declination over 28º40' isn't observed anymore (Astropixels.com).
The biggest parallax impact on Moon’s extreme declination will be around the moment of perigee. Usually, there is about a day or two difference between the biggest approach the Moon to the Earth, and the lunar extreme declination. There are really rare cases, where this coincidence might happen within the span of a few hours only. In the current span of 1000 years, we have 2 situations like this on February 12, 1597, and February 26, 1793. The primary reason, which explains the relatively bigger frequency of events such as this is the larger Moon’s declination, exceeding the threshold value of 28º40′ more often. As a consequence, more than 2 major lunar standstill events were considered. We must be aware, that a situation such as this is quite typical for lunations directly preceding the maximum of vernal lunar orbit perturbation every 93 years. They tend to be observed in February or March. Much more often the coincidence applies to the lunar apogeum, when the value of parallax is the smallest. Indeed, we are still talking about the span of 93 years, but the major lunar standstill is more aligned with the moment of apogee than the perigee. By about 38 years from now, we should expect the biggest synchronization between these 2 events, which will be separated only by just 2 hours in 2062.
Lunar parallax has an impact on the size of the Moon’s arctic circle, which changes slightly. For greater parallax, the latitude from where the circumpolar Moon can be seen is imperceptibly closer to the pole contrary to the situation, when the extreme declination occurs near the apogee. Then the Moon as the circumpolar celestial body can be seen further from the pole. Let’s consider it in the example below.
Spinarnir is the southernmost hill of Faroe Islands which is located pretty much exactly at the Moon’s arctic circle. The image below shows several single occurrences of the Moon passing through the local meridian in the north during the current 2024-2025 major lunar standstill in comparison to another major lunar standstill, which coincides with the perigee (Pic. 22).
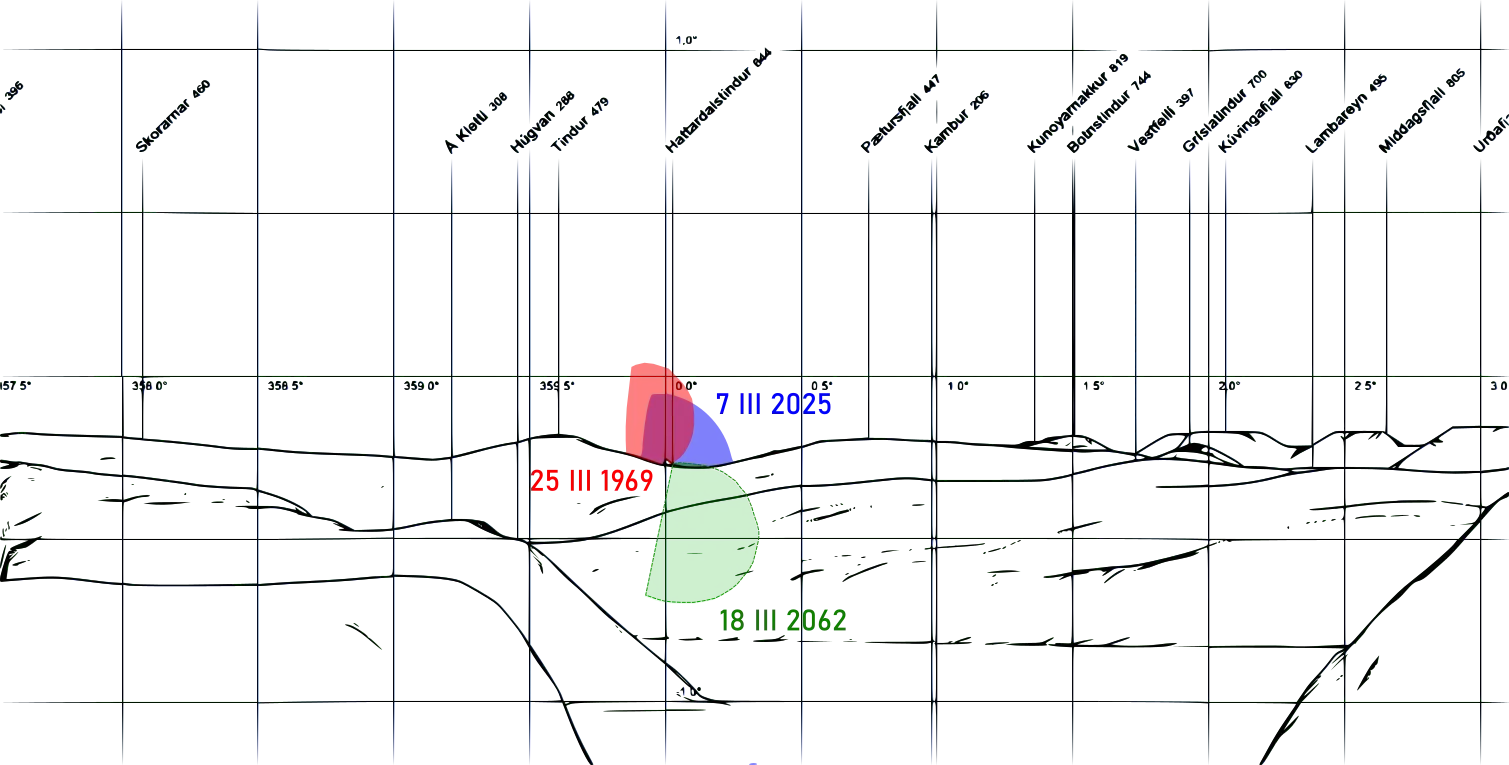
Pic. 22 The visualization of the Moon’s lowest point, which could be seen from the Spaafelli 462m.a.s.l. [61° 25′ 32.88″ N] one of the southernmost hills located at Suðuroy island (Faroe Islands) with a view at Hattardalstindur 644m.a.s.l. located 96km away behind which the Moon will be visible on March 7, 2025 morning in comparison to the nearest major lunar standstill periods, which occur around lunar perigee or apogee (based on Peakfinder.org).

Pic. 23 The view of the Moon during the most extreme declinations of 1969, 2025, and 2062 major lunar standstill from the top of King George Island [- 61° 58′ 51.7 S] (based on Peakfinder.org).

Pic. 24 The visibility of the Moon during the 2025 major lunar standstill from St George Island [- 61° 58′ 51.7 S] in northern and southern directions is estimated at the main dates of most extreme declinations (based on Peakfinder.org).

Pic. 25 The visibility of the Moon during the 2025 major lunar standstill from Suðuroy island [61° 25′ 32.88″ N] in northern and southern directions is estimated at the main dates of most extreme declinations (based on Peakfinder.org).
The images above (Pic. 22-23) consider the various altitudes of the Moon at its lower point as expected during three separate major lunar standstills 1969, 2025, and 2062. The most extreme declination of March 7, 2025, reaches the declination value of 28°42’36”. The analogic situation from March 25, 1969, features the declination of 28°43’30” and the other one from March 18 2062 the least extreme declination of 28°40’18”. Just a tad further north Moon’s declination on March 25, 1969, should make it unnoticeably higher than in 2025. Because of the apogee, which occurs on the same day, the range of Moon visibility above the horizon is wider, so that means it is the best visibility from both considered locations. From the Spaafelli the lunar upper limb doesn’t go under the geometrical horizon. Moreover, because of the apogee the quarter Moon tends to look smaller at the horizon. The date of March 18, 2062, shows quite the opposite situation because the extreme declination north occurs less than 48 hours before the perigee. The perigee means, that the range of Moon visibility above the horizon is slightly narrower. The same as in the case of apogee, the situation is shaped by the lunar parallax. Once lunar parallax is the biggest (around perigee) the Moon goes below the horizon slightly earlier than it could be from a geocentric point of view. This is why the body cannot be observed from the locations lying mathematically at the Moon’s polar circle. At the location in Faroe Islands, only the upper limb of the Moon will be visible at its lower point. A slightly different situation will be observed at a similar time at St George Island, where the observer could spot around half of the Moon’s disk. This is because of the less extreme declination of 28°40’18”.
Other images (Pic. 24-25) represent the same places but with a look at 2 opposite directions – north and south where the Moon can be observed exactly at the horizon during its extreme declinations on March 2025. As you see the local topography has a valuable influence on Moon visibility and marks locally the lowest latitude from which an observer can see the circumpolar Moon or just a partially visible lunar disk lingering at the horizon for a while.
6. THE APPLIANCE OF MAJOR LUNAR STANDSTILL FOR LONG-DISTANCE OBSERVATIONS
There are a multitude of publications describing the relation between the lunar standstill and megalithic constructions located across the UK and other parts of the world. There is information about the extreme azimuth of moonrise or moonset defined by some part of megalithic construction or local horizon feature located close to the historical place. There is no information about the appliance of a major lunar standstill to the development of long-distance observations unlike of multitude of local places for which the phenomenon has been deeply analyzed. Indeed, the best approaches based on closer horizon features can be found in the pioneer publication of Megalithic Lunar Observations issued over a half-century ago, which was followed by other archeoastronomy publications later. The best way of understanding the issue is the image below.
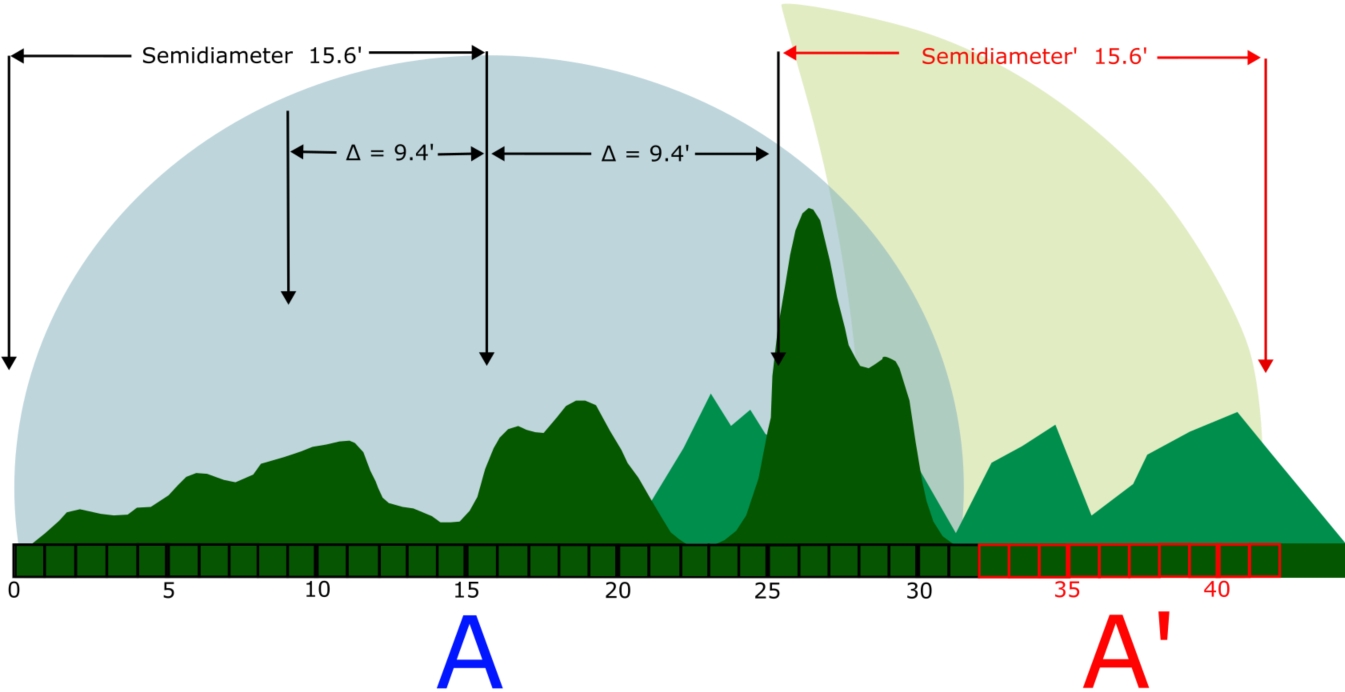
Pic. 26 Graphical representation of the distant horizon features against the major lunar standstill perturbations (based on Thom, 1971) Translating it into the long-distance observations appliance, we can assume, that the X-axis values represent the arc minutes from 0 to 42′. The first 32 arcminutes correspond to the mean angular diameter of the full Moon, which is observed around the moment of minimum perturbation. The other 10′ apply to the quarters reaching the distant horizon at extremal azimuth during the maximum perturbation. The arrows depict the changes in setting Moon driven by its orbit perturbation, where: A – the full Moon during a moment of minimum perturbation; A’ – the first quarter Moon during a moment of maximum perturbation.
The histogram itself is a result of analyses of observed lunar declinations, about which you can find more in the Megalithic Lunar Observations publication and it has been adapted for watching the distant landscape features by setting the Moon. Let’s assume, that this alpine-looking range located about 200km away from the observer has a similar angular size to the size of the Moon at its mean distance. However, it’s impossible to see most of this range a front of the setting Moon, A situation like this could be theoretically plausible only when the most extreme declination of a major lunar standstill takes place around the moment of the moonset. Even so, the right part of the range with the northernmost azimuth won’t be visible on every lunation due to lunar orbit perturbation. Practically it will happen only around the first quarter of the Moon, when the lunar orbit inclination reaches maximum. An opposite situation could be reflected in the moonrise time around the last quarter of the Moon (September), although the Moonset is easier to observe because we can track the body in the sky a bit later. Once all the discussed factors are favorable, the setting of Moon’s limb could be observed even beyond 42′. It could happen presumably in the situation, when:
– the lunar parallax is the smallest (for northernmost azimuth, major lunar standstill coincides with the apogee) or the biggest (for southernmost azimuth, major lunar standstill coincides with the perigee)
– the Moon reaches its extreme declination when setting beyond the horizon
– significant astronomical refraction takes place.
Let’s consider this situation in some live examples below.
The appliance of major lunar standstill declination extremes can bring the explorative approaches, as the Moon can set behind the objects never observed from the given location. It’s possible beyond the daylight and twilight conditions when the terrestrial refraction can be potentially the most favorable. As mentioned earlier, the most significant terrestrial refraction occurs as night approaches, when the ground radiates the warm into the air. There are some observations made overnight, which prove extraordinary refraction conditions over lowlands. The major lunar standstill allows chasing some distant landscape features at azimuths, which wouldn’t be possible on another occasion. Let’s consider the case study below. The Świętokrzyskie mountains are geologically the oldest in Poland. They are located approximately 100km from the northern edge of the Carpathians. Some Carpathian ranges are high enough to be visible well from those mountains. We should point out especially Tatra Mts – the shortest Alpine range in Europe, which is located over 200km from Swietokrzyskie mountains. The second highest group in Polish Carpathians is Beskid Żywiecki, including the Babia Mountain called informally the “mother of bad weather”. Unfortunately, neither Tatras nor Babia have azimuth, that the Moon could reach in any way. The second-highest mountain in Beskid Żywiecki – Pilsko is located exactly 193km from the easternmost point of the Lysogóry range, which is the highest one in the Świętokrzyskie Mountains. The place is also the local centre of pilgrimage as the remarkable Holy Cross monastery is located there. This is admittedly the only spot in the Lysogóry range, which allows us to see the moonset behind the Pilsko mountain located 193km ahead (Pic. 15).
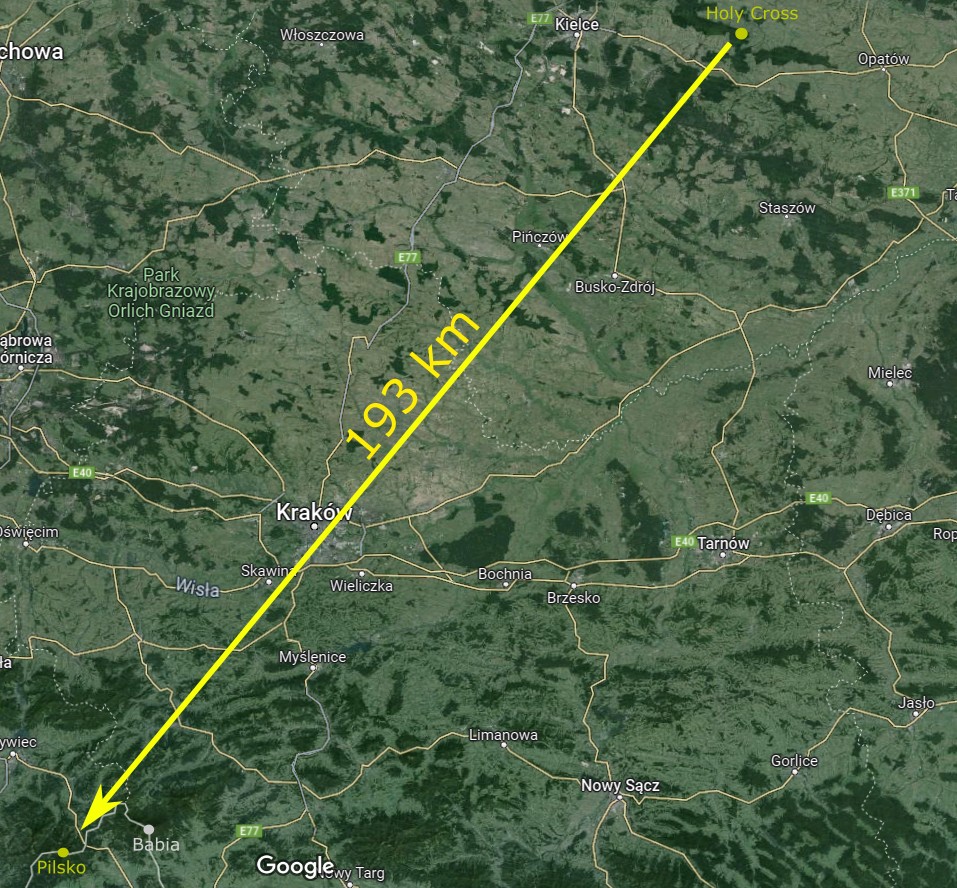
Pic. 27 The line of sight between the Holy Cross (Swietokrzyskie mountains) and Pilsko (Beskid Zywiecki) at which moonset is possible during the extreme south major lunar standstill (maps.google.com).
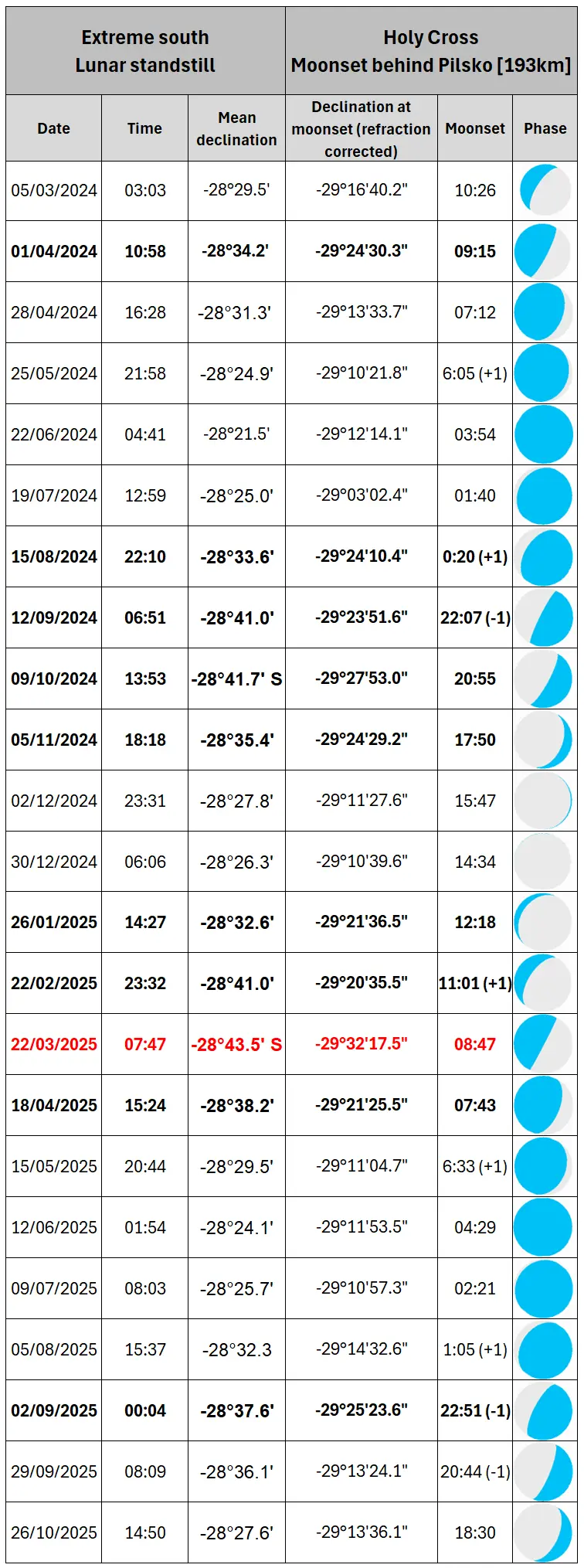
Now, let’s consider the chance of seeing the moonset behind this remote mountain during the current major lunar standstill period (Tab. 9), where the emboldened text marks the days when the Moon’s limb at least grazes the peak and the red one marks the best moonset.
Tab. 9 The extreme south major lunar standstill 2024-2025 circumstances (local time) concerning a possible moonset behind the Pilsko mountain located 193km away from the Holy Cross monastery.
Considering the mean declination obtained i.e. from the Astropixels.com service we shall expect the moonset behind Pilsko in the vast majority of cases when the lunar declination is lower than -28º32′. However as you already know, the coincidence of extreme declination with moonset (or at least short span of time between them two) is necessary for this phenomenon. Therefore, knowing the true Moon’s declination is much more important when setting behind the horizon. On top of that, this declination should be corrected by the parallax and (at least) atmospheric refraction. In turn, we can be assured about the final declination value, which makes this view possible from this particular place. Assuming, that you are standing near the monastery, the moonset behind Pilsko should be possible for all the declinations south of -29º20′ regardless of the lunar position against the most extreme declination point reached on its way. The animation below concludes the ongoing 2024-2025 major lunar standstill, which counts 10 events like this (Pic. 28).
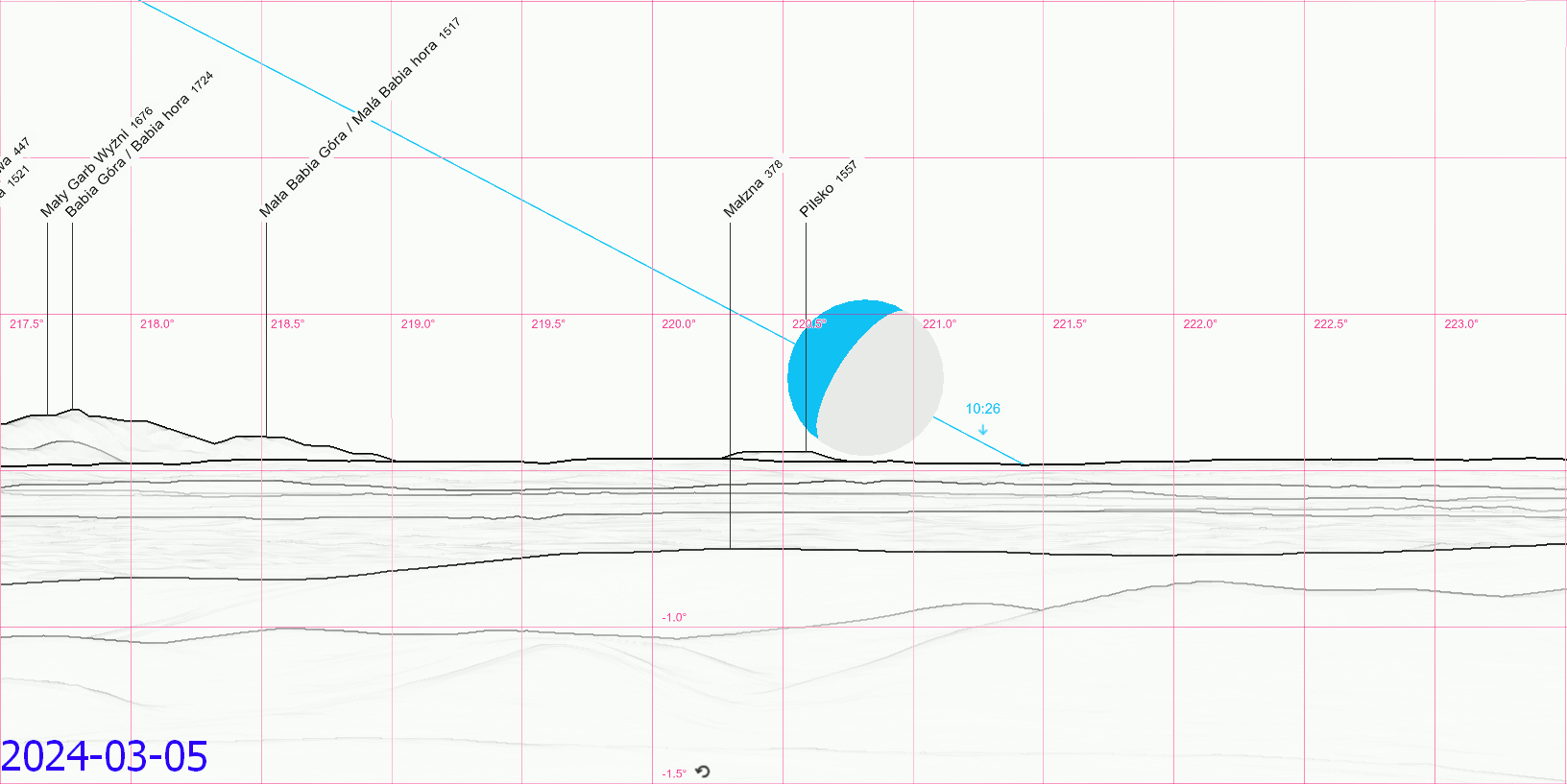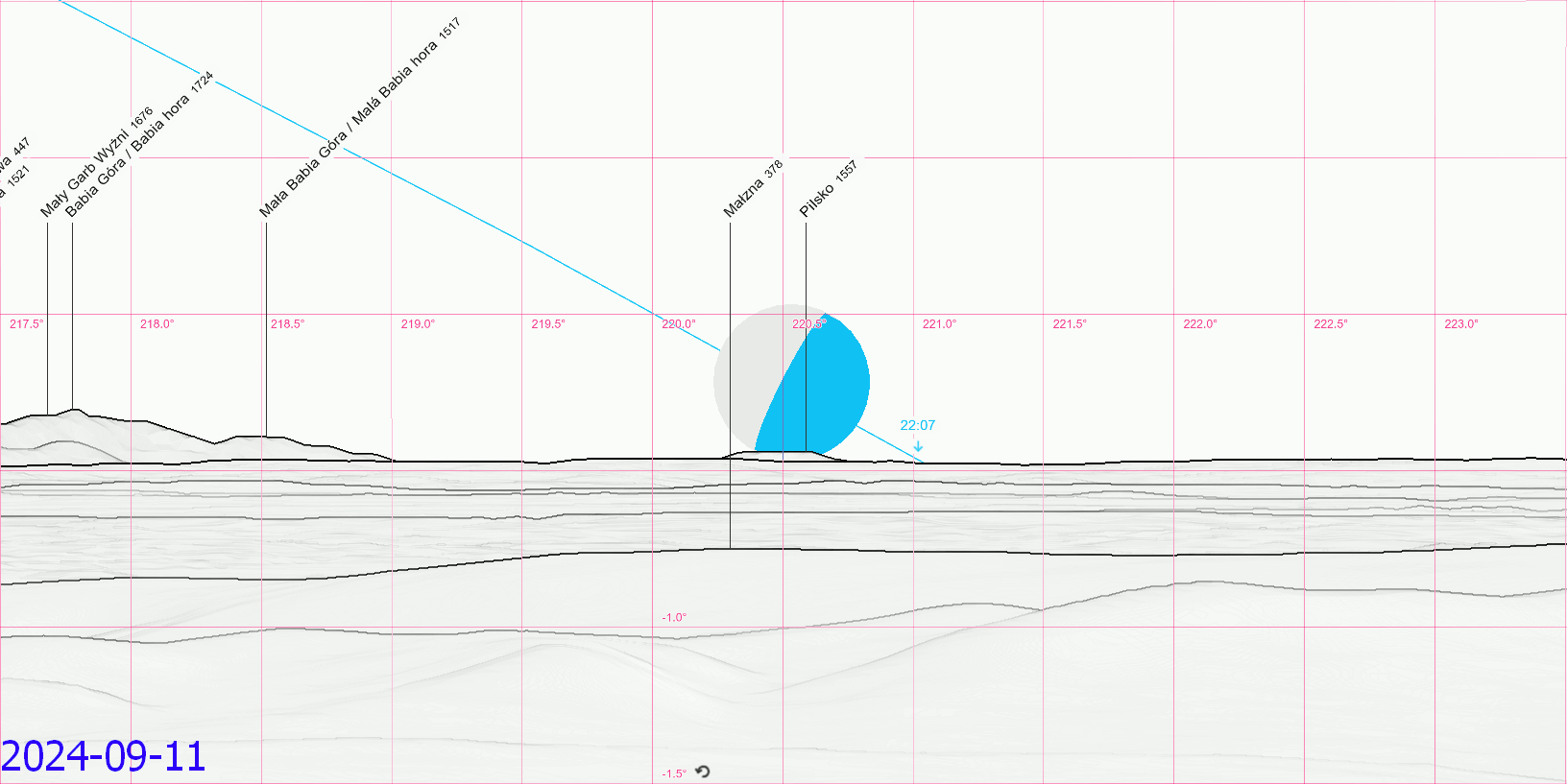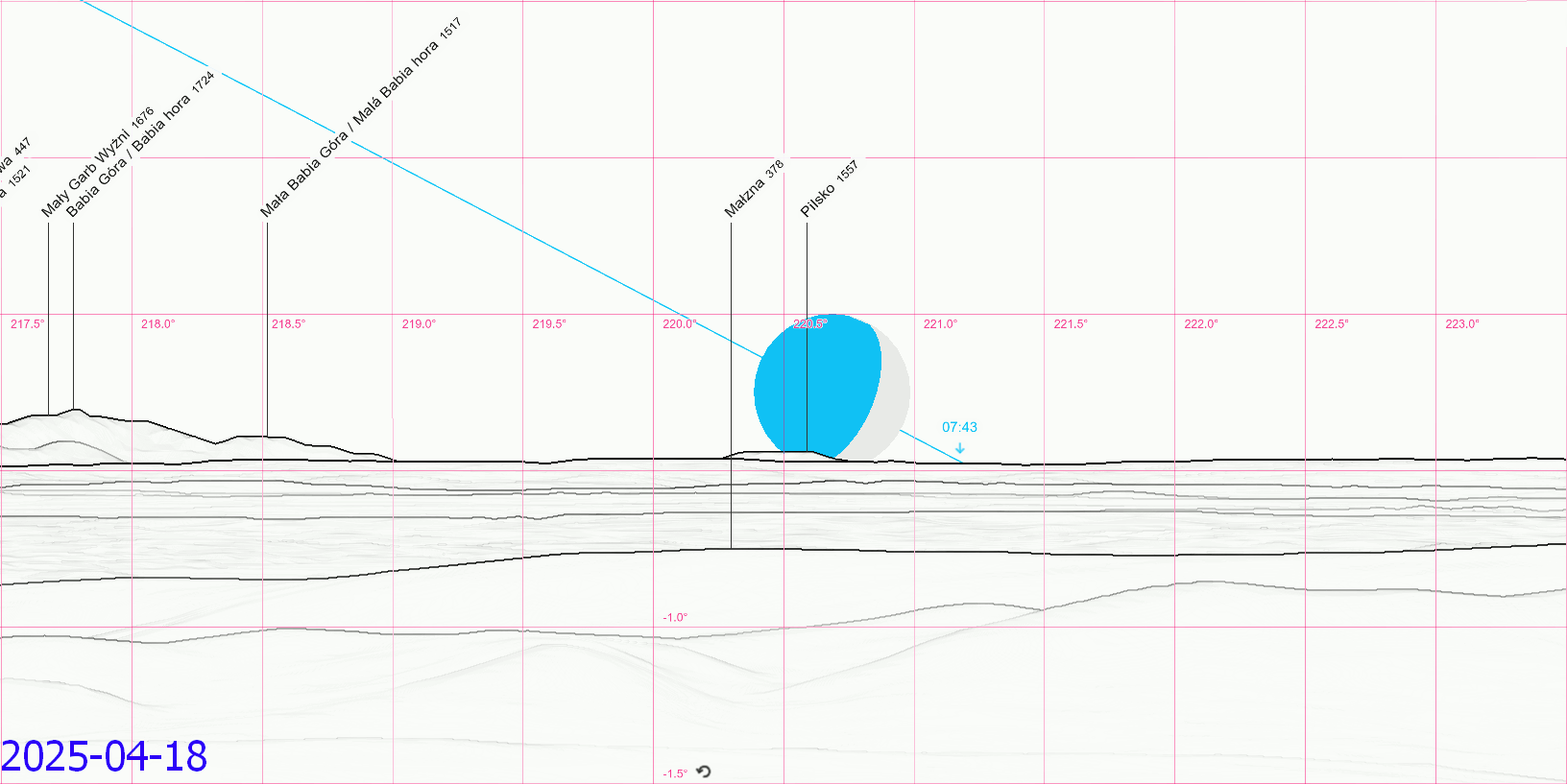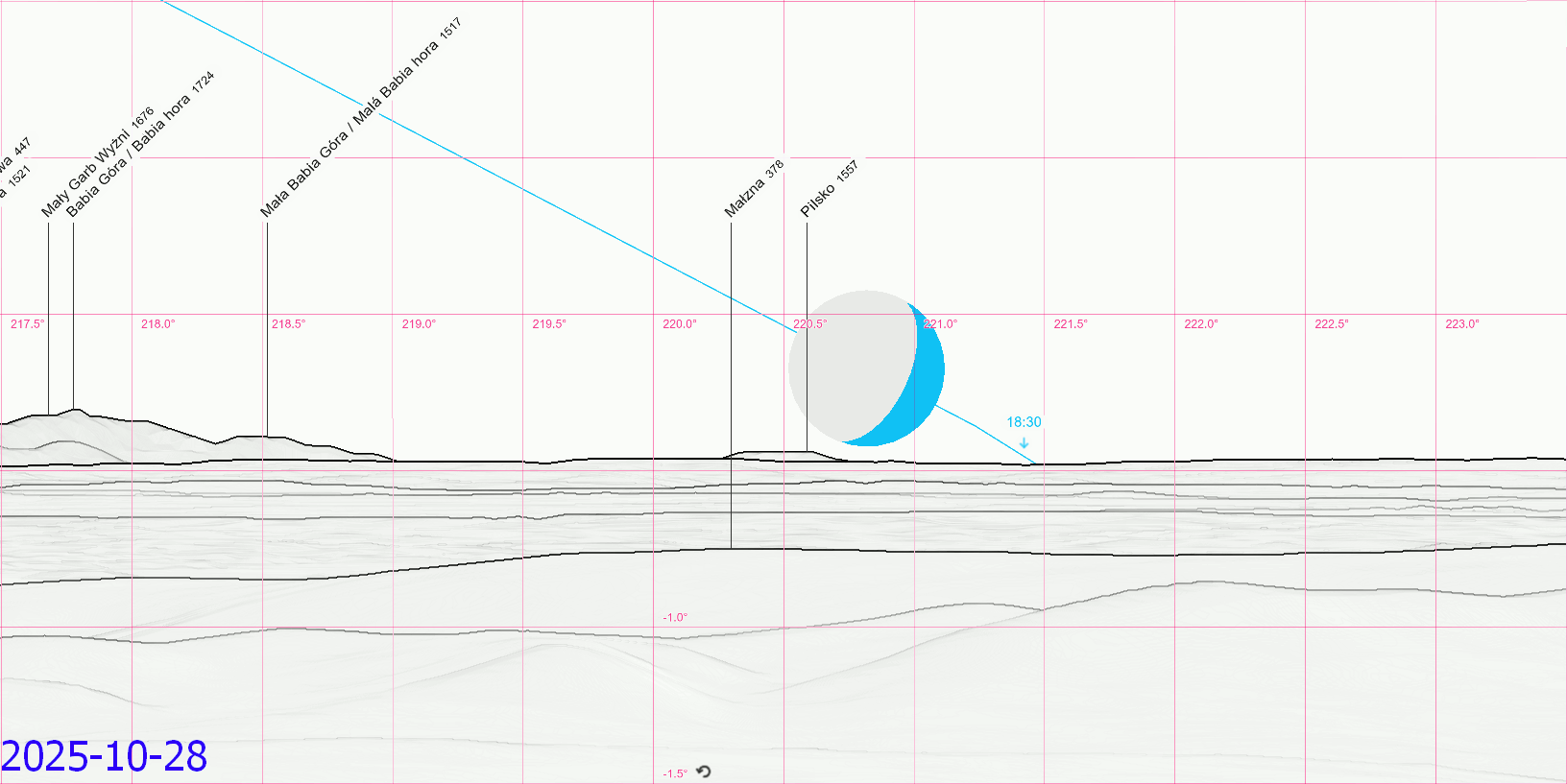
Pic. 28 The major lunar standstill south 2024-2025 with a possible moonset behind Pilsko mountain at a distance of 193km from the Holy Cross monastery (Peakfinder.org).
Within these events, we can point out the moonset azimuth typical for minimum and maximum lunar perturbation typical for March-April & September-October, and June (or December, although the new moon wasn’t considered as it’s rather invisible) (Pic. 29).

Pic. 29 Some most extreme moonset positions during the 2024-2025 major lunar standstill as seen from the Holy Cross mountain, typical for moments of minimum and maximum lunar orbit perturbation (Based on Peakfinder.org).
The analysis leads to the graphical conclusion of the south extreme moonset azimuth range, which is typical for nearly a year and a half major lunar standstill series (Pic. 30).

Pic. 30 The extreme south moonset azimuth range is possible to see from the Holy Cross mountain during a major lunar standstill. When the lunar orbit perturbation reaches its maximum (MAX), the around quarter Moon can set behind the Pilsko mountain, which is 193km away. Unfortunately, the set of a full Moon isn’t possible as it occurs at the minimum lunar orbit perturbation (MIN).
Worth attention is the extreme declination on February 22. Because it occurs shortly before midnight local time, we effectively should expect two moonsets at very similar azimuths. The moonset on February 23 in the late morning will graze the distant Pilsko whereas the preceding one around 23 hours earlier is a near-missing one. Both won’t be visible as they happen in full daylight. By looking at the sketch below (Pic. 31) we can even notice, that these 2 paths are closer to each other near the horizon, which is the best proof of rapid lunar declination changes as discussed earlier (Pic. 9).
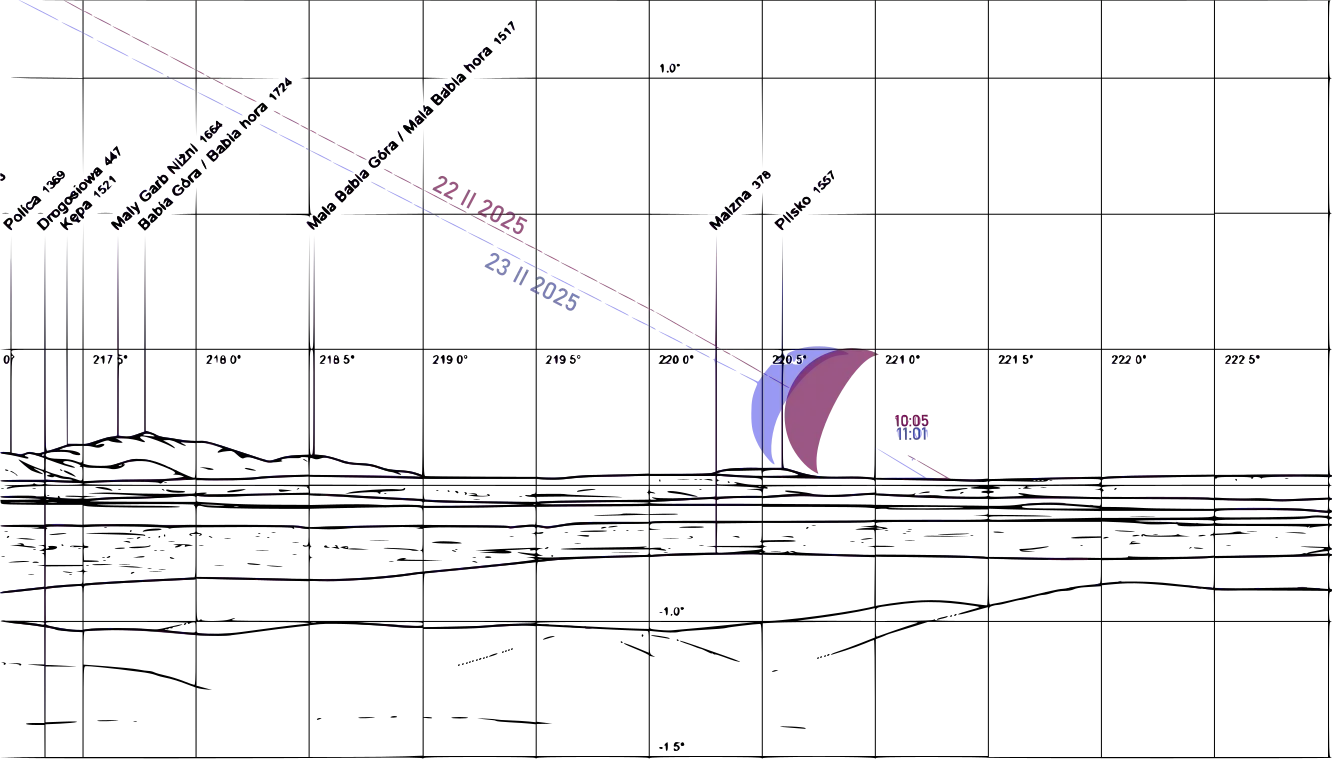
Pic. 31 Twin moonsets on February 2025 separated by the extreme southern declination approximately 11 hours between each other. As a result, the first one near-misses Pilsko and the latter one grazes the peak only. The lunar paths in the sky are closer to each other near the horizon. Since the declination of the Moon on February 22 will decrease, on the next day it will increase (Peakfinder.org).
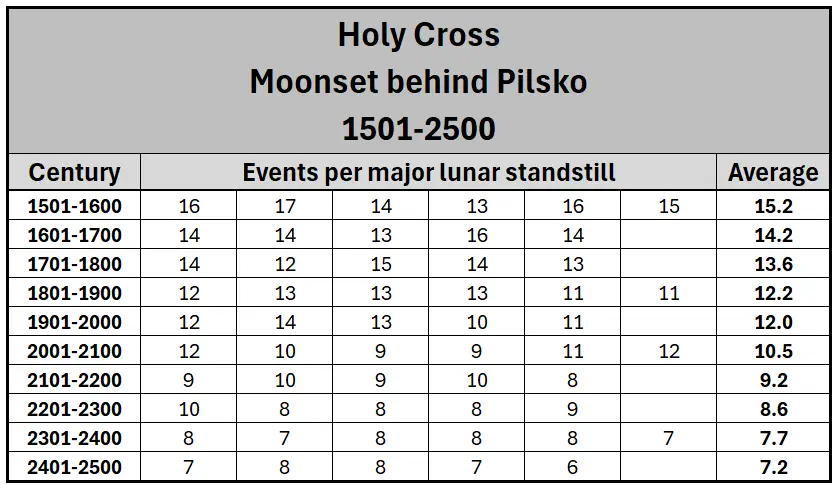
Because of decreasing the Earth’s orbit inclination we can assume, that the lunar limb will eventually graze this distant landscape feature for the last time in ages. The table below presents the exact number of potential events, that would have happened when the mean declination of the Moon is more extreme than -28°32′ (Tab. 10).
Tab. 10 The presumed number of times when the Moon can set behind Pilsko (193km) as watched from the Holy Cross mountain per one period of lunar standstill across 1000 years between 1501 and 2500 (based on Astropixels.com).
The period of 1000 years reveals a significant decrement in these events, which are over twice as rare at the end of this period. By leading this computation for further centuries we shall assume, that the last event when the Moon’s limb grazes Pilsko would occur around AD3500. Next, this event wouldn’t be observable for centuries from this location. On the other hand worth attention is the graph below, which shows how these events could have looked earlier in history. In megalithic times the Moonset could be visible even behind the lower Babia hill (Mała Babia Góra) (Pic. 32). The Image below shows the estimations with assumption at the same time against the peak of extreme lunar declination.
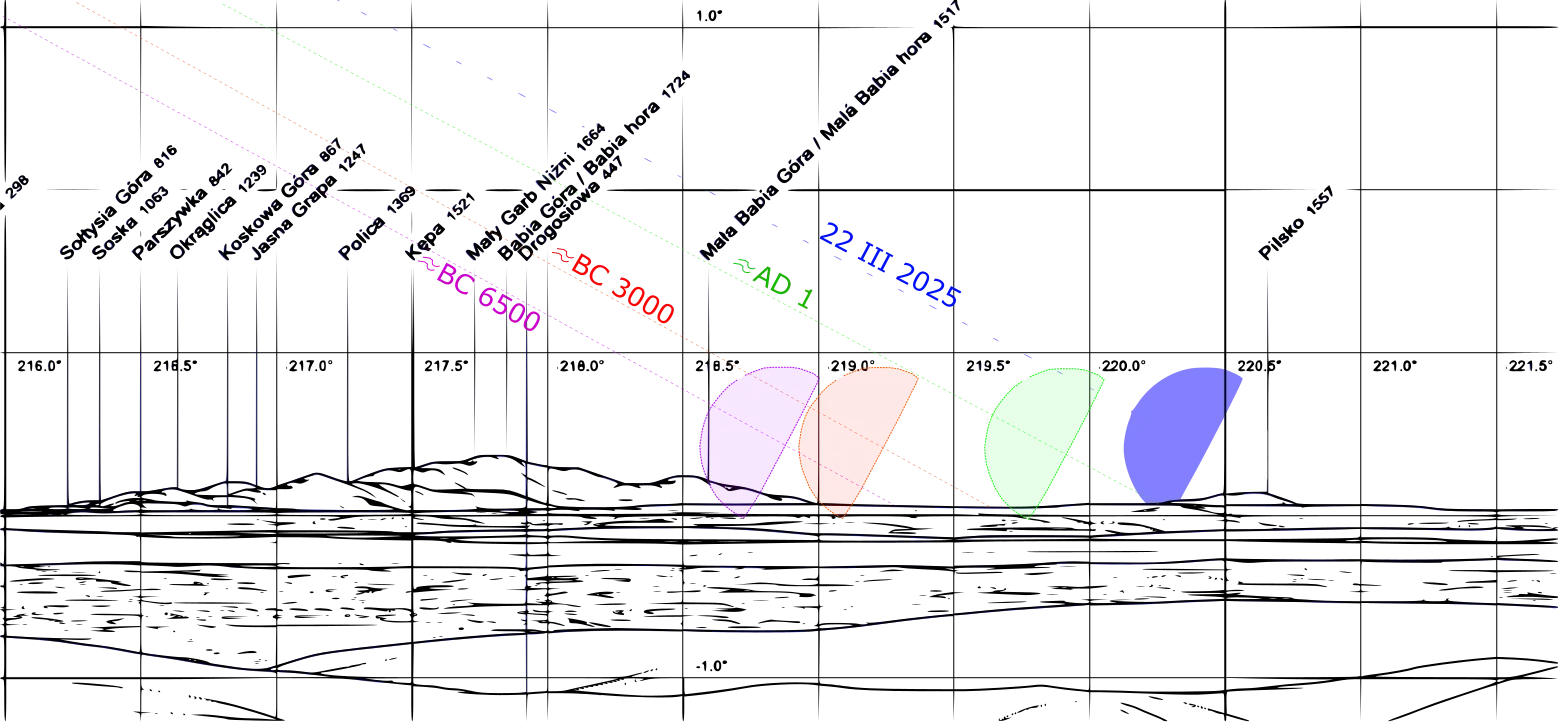
Pic. 32 The extreme south moonset azimuth as could be observed from the Holy Cross mountain in historical times. The quarter Moon used to set behind the little Babia hill slopes yet around 5000 years ago (based Laskar, 1986 and Peakfinder.org).
Let’s consider an opposite example with the extreme north moonset azimuth on March 7, 2025. This time our hypothetical observation is based in Italy in Parma province at one of the Apenninian summits – Monte Cervellino. The mountain offers nice long-distance views of the Alps. On March 7 the Moon is estimated to be set behind the Matterhorn (Monte Cervino) peak at a distance of 246km (Pic. 33).

Pic. 33 The extreme north moonset azimuth as could be observed from the summit of Monte Cervellino (Apennines, Italy) in historical times. The quarter Moon used to set behind the Dufourspitze located 234km away from this place yet around 4000 years ago. Nowadays we can enjoy at least a few moonsets behind the Matterhorn during the major lunar standstill period (based on Laskar, 1986 and Peakfinder.org).
In historical times for several thousand years, the northernmost azimuth of moonset could be observed behind Dufourspitze 4634m.a.s.l – the highest summit of Switzerland located 234km away. Because of the reason explained earlier in this article, moonsets such as these haven’t happened anymore since around BC 2000. Again, the computation has been based on consideration of the same time of moonset against the time when the most extreme north declination is observed.
In other cases, where in fact computations of extreme moonrises or moonsets can be useful play around the distant landscape features not visible normally, but only under abnormal refraction conditions. The extreme moonrise/moonset azimuths can help with identifying potential objects, that aren’t visible through the thickness of the atmosphere even if refraction takes place. Moreover, the moonset happens at various moments of the day unlike the sunset, which can be translated to different meteorological conditions and finally the refraction coefficient. There are some incredible long-distance observations carried out overnight, which proved extremely abnormal refraction. I believe the setting Moon is the other factor, which can help with unveiling distant mountains hidden beyond the geometrical horizon and never observed before from the given place. I’ve prepared some examples before, which include a couple of cases with different refraction values and cover the most favorable moonset azimuths.
Let’s consider the example of the place, where the observation report exists already. This is located in Polichna [50° 48′ 56.53309″N, 22.318993426568856 E] (Pic. 34), from where the High Tatra range can be seen at a distance of approximately 236km by the refraction coefficient of 0.21 or even more, which hasn’t confirmed yet.
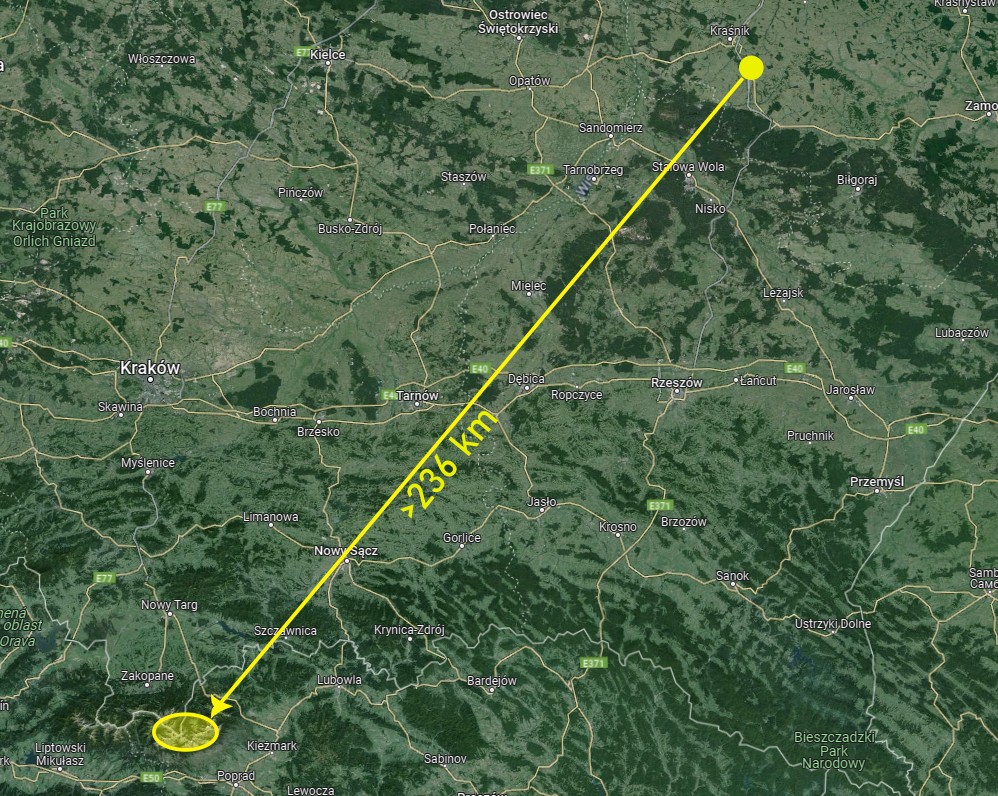
Pic. 34 The approximate distance from Polichna village to High Tatra mountains rising at an azimuth of moonset during the major lunar standstill (maps.google.com).
As the very first step I would advise to confirm, that the moonset can occur at the given azimuth. The quickest way for assumptions such as these is using the PhotoEphemeris application, which can draw the estimate azimuths of the Sun and Moon for you (Pic. 35).
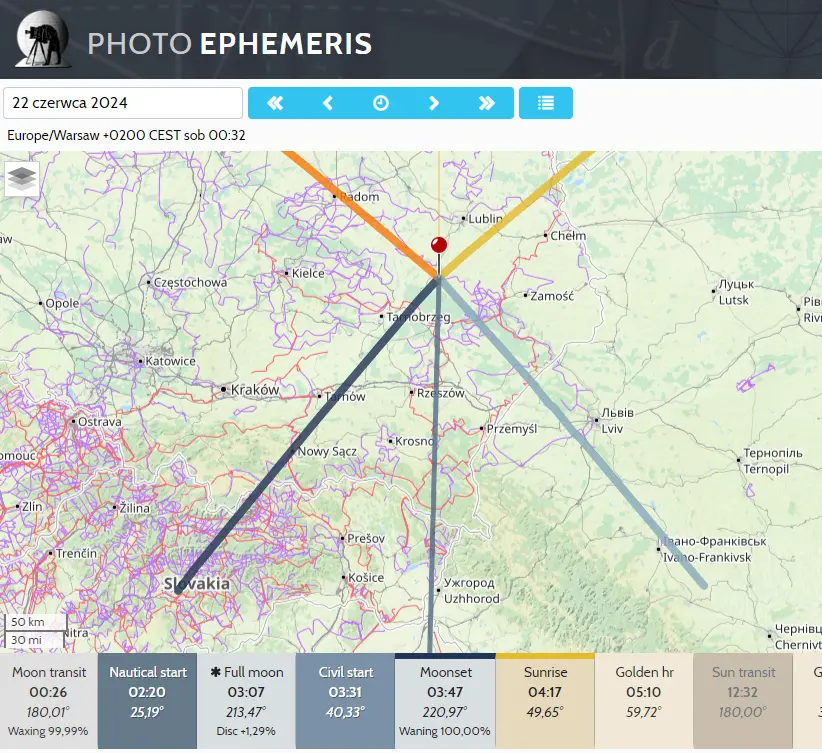
Pic. 35. The quick insight into the azimuth of moonrise/moonset from the interesting location by using the PhotoEphemeris application.
Next, if we are sure, that the moonset occurs at the estimated azimuth, our best approach is to use the combination of Peakfinder.org and Udeuschle panorama generator. The Udeuschle panorama generator is more precise for extremely distant landscape features and, what is more important, we can render the various refraction coefficients by the method described here. Prior to it, let’s analyze the exact moonset azimuth with the Peakfinder.org website. Next, use the 10x zoom enlargement (Telescope mode) in the Udeuschle panorama generator centering at the same azimuth range. You will find the possibility of a moonset behind the distant landscape feature by the terrestrial refraction conditions. The image below shows how to make it right (Pic. 36).
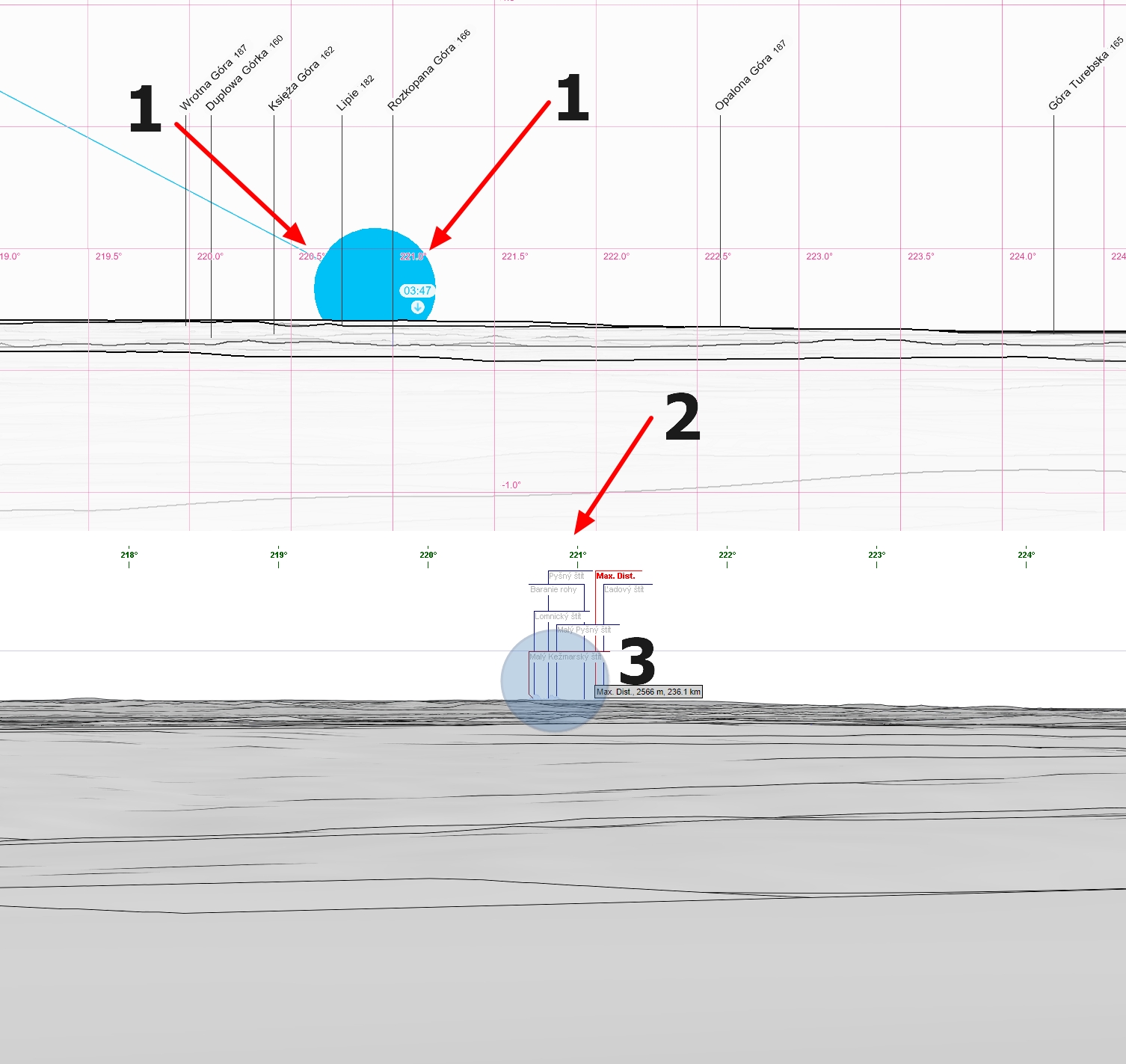
Pic. 36 The comparison of moonset azimuth shown by Peakfinder.org with the distant landscape features rendered by the Udeuschle panorama generator for the refraction coefficient of 0.23

Pic. 37 The estimated moonset azimuths during the 2025 major lunar standstill as seen from Polichna village. The lunar limb will set straight behind the High Tatras, which visibility will depend on the terrestrial refraction coefficient up to 0.3 (based on Udeuschle.de)
Let’s consider another example in Romania. The Releul hill in Meses range [47° 9′ 8.96439″ N, 23° 6′ 4.76166″E] rises above the Zalau town (Pic. 38).
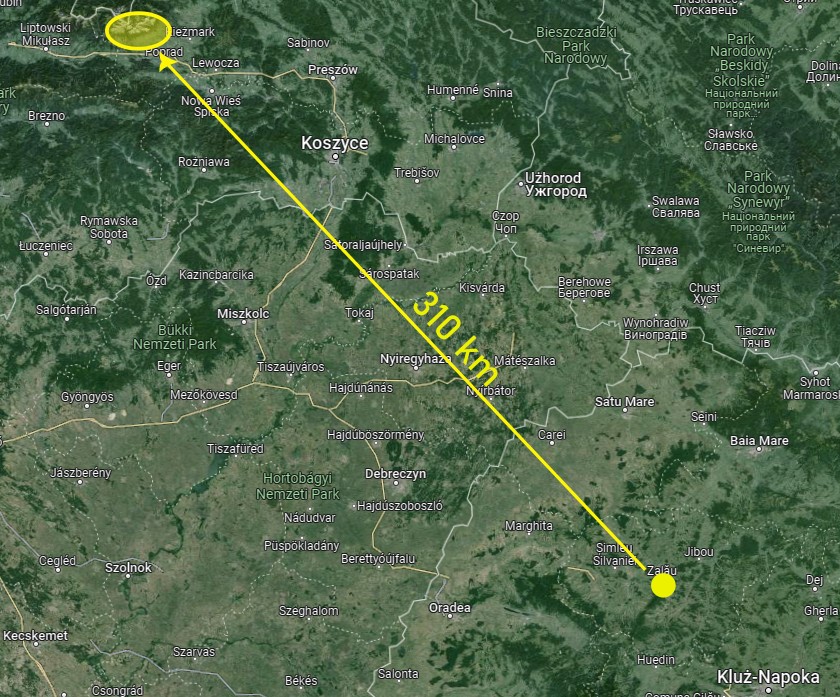
Pic. 37 The approximate distance from Zalau town to High Tatra mountains located near the azimuth of the moonset during the major lunar standstill (maps.google.com).
Again, as the very first step I would advise to use the PhotoEphemeris app, which can draw the moonrise/moonset azimuths for the given day quickly. (Pic. 38)
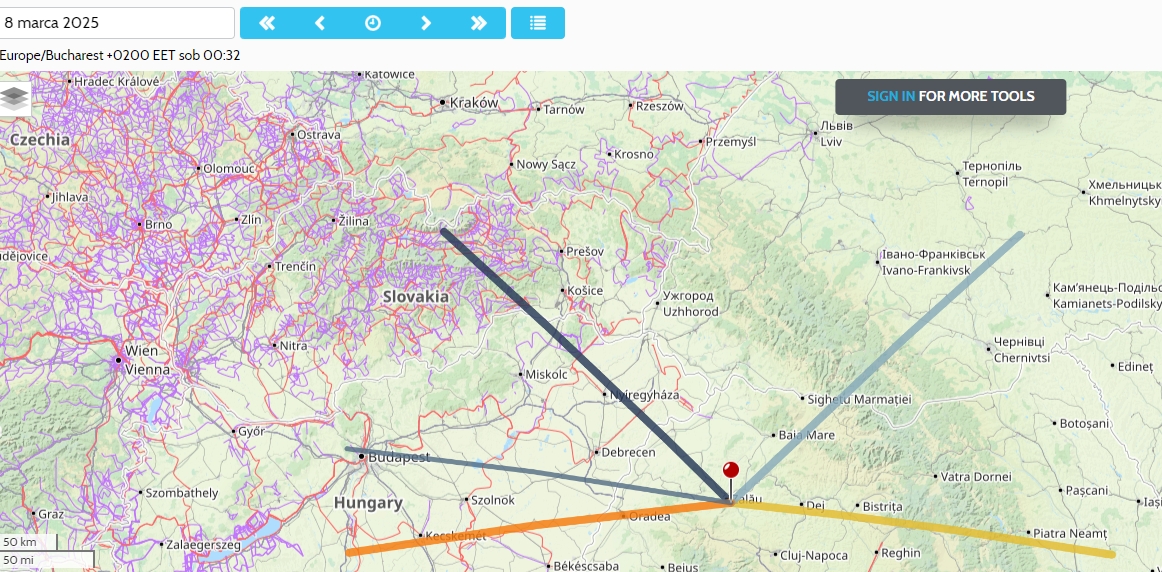
Pic. 38 The most extreme moonset azimuth from Zalau town in Romania during a major lunar standstill App.photoephemeris.com).
Considering the extreme refraction coefficient of 0.4 this place gives an extremely rare chance of seeing the High Tatra range. However, it’s not possible to reach it by the Moon (Pic. 39).
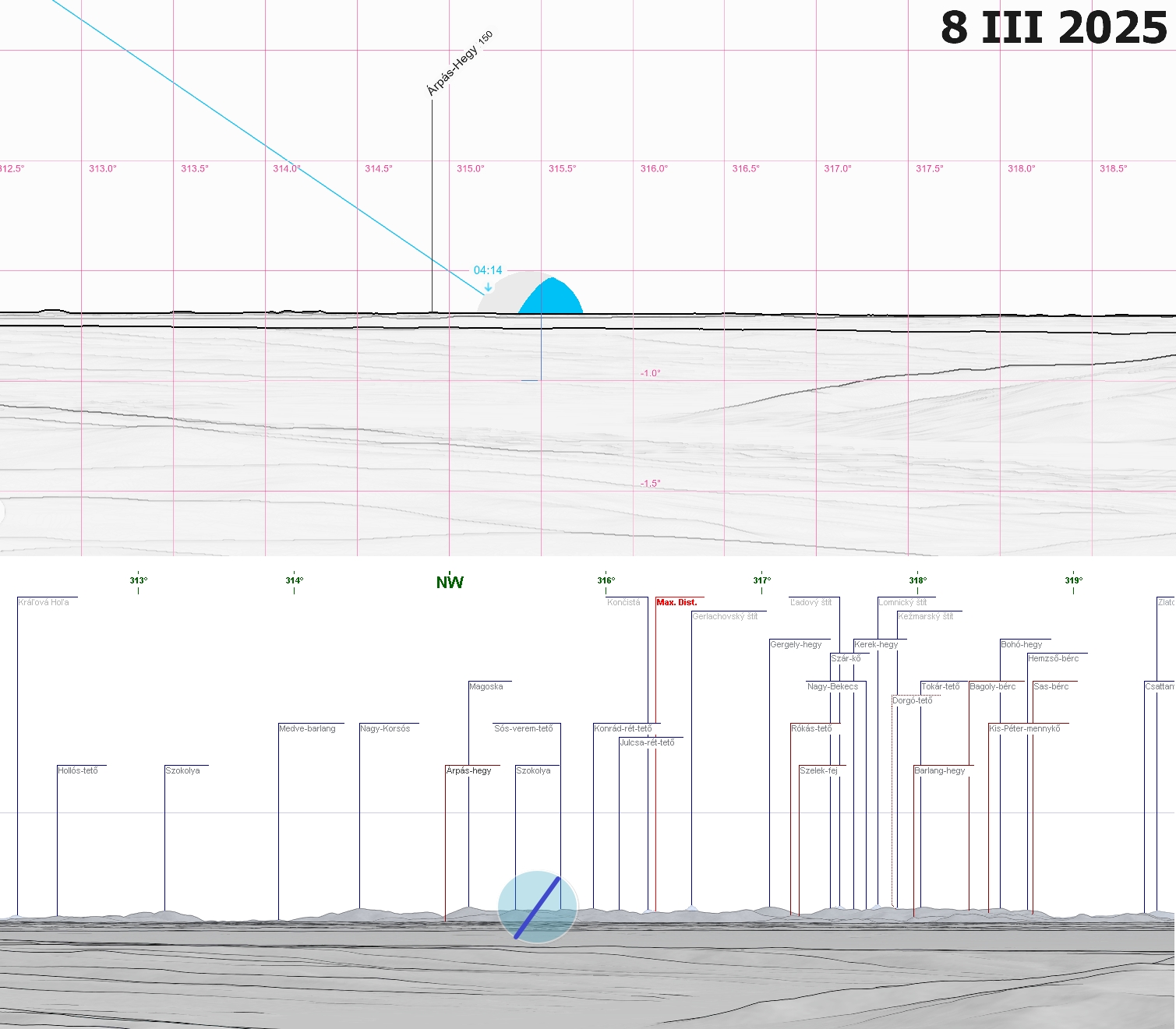
Pic. 26 The most extreme moonset from the Meses range above Zalau town won’t be enough for grazing distant High Tatra mountains, although it was possible in megalithic times when the refraction coefficient could have reached 0.4 (Peakfinder.org/Udeuschle.de).
The method described above can be used anytime regardless of the Moon’s declination.
Another thing is the moonlight reflected by the Earth’s atmosphere. The mechanism is the same as in the case of setting Sun. Shortly after the Sun goes down below the horizon the contrast between the illuminated sky and the shaded horizon is the best. Indeed, in the case of the Moon, the occurrence is restricted to the narrow range of angular depression, as the body isn’t bright enough. The influence of moonlight is estimated to be observed down to a lunar depression of 6°. The lunar twilight period won’t produce the same effect as the solar one though, but the Moon is bright enough to enlighten its angular vicinity at the moment when it sets or rises. The effect, for sure, won’t look great in the sky and line of sight polluted by artificial light, however, the presence of high clouds can be helpful even in this situation. This particular matter will be a subject of study in the future.
7. SUMMARY
The article presents a strong outreach to the major lunar standstill occurrence, which is sometimes called the once-a-generation event observed only every 18,6 years. Unlike the minor lunar standstill, which is rather featureless as far as the subject of this text is concerned, the major lunar standstill is worth significant attention. There are at least 2 reasons behind it, where the first one is undeniably the occasion of seeing the Moon rising or setting above more extreme azimuth compared to the solstices. Another one states the rarity of this event as it happens only 5 times per century (sometimes 6). Indeed lunar standstill isn’t a single event, because is observed in series for about a year and a half period, although there is a long, at least 17-year duration, where the moonrise/moonset azimuths aren’t extremal. On the other hand, for more than 9 years the Moon can rise and set more extremally to the Sun during solstices, especially in favorable parallax conditions widely discussed in this article. Seeing the body rising or setting behind some specific features or objects on the horizon is really interesting, as a multitude of observations proves it. This occurrence was probably widely known in ancient history and, on top of that, often revered by rising a multitude of objects intentionally oriented into specific azimuths as well as probably also some ritual human behaviors and beliefs, which could have been passed between the generations. Nowadays, unfortunately, the major lunar standstill period seems to be forgotten and underrated. Thereby I would add the third reason why a major lunar standstill should be taken into account seriously as an interesting astronomical event. Namely, the matter of distant or even extremely distant horizons unlike the closer one considered in all the publications about it. This is the thing, which has never been raised before. The studies about the maximum range of view from the given point by the occurrence of a major lunar standstill can bring invaluable information about the terrestrial refraction behavior during the night. On the other hand, the moonset or moonrise above the section of the horizon, where it’s not seen so often can be a nice observation even without any equipment. During this period we can assume, that naked-eye horizon astronomy cannot distinguish any observable differences in standstill horizon limits during the course of the standstill year (Reijs 2003). If this is so, we can attend to the given observation several times and track the Moon’s path, which will be helpful with centering our equipment toward the interesting azimuth later on.
Mariusz Krukar
References:
- Astronomical Almanac for the Year 2010 and Its Companion, United States Naval Observatory, U.S. Government Printing Office
- Berger A.L., 1976, Obliquity and Precession for the Last 5000000 Years, (in:) Astronomy and Astrophysics. 51 (1): 127–135
- César Gonzalez-Garcia A., 2016, Lunar Extremes, Lunar Cycles and the Minor Standstill, (in:) Journal of Skyscape Archaeology
- Ellingson E., Silva F., 2024, The Major lunar standstill season is here!, (in:) Journal of Sksycape Archaeology 9(2): 281-288.
- Espenak F., Meeus J., 2009, Five Millennium Catalog of Solar Eclipses: –1999 to +3000 (2000 BCE to 3000 CE)—Revised, National Aeronautics and Space Administration, Goddard Space Flight Center Greenbelt, Maryland 20771
- Gough T.T., 2014, Further evidence for the existence of prehistoric celestial alignments in western Scotland: Calendrical alignments on the Island of Mull, (in:) Mediterranean Archaeology and Archaeometry, Vol. 14, No 3, pp. 247-257
- Gough T.T., 2018, Refraction and precise lunar alignments, (in:) Mediterranean Archeology and Archaeometry, vol. 18, no.4, p.435-440
- Laskar J., 1986, Secular Terms of Classical Planetary Theories Using the Results of General Relativity, (in:) Astronomy and Astrophysics. 157 (1): 59
- Magli G., 2016, Archaeoastronomy: Introduction to the Science of Stars and Stones, II Edition, Springer, Milan
- McCluskey S C., 2017, Archeoastronomy and refraction near the Earth’s surface, (in:) Journal of the History of Astronomy, vol. 48, no.3, pp. 329-345
- Meeus J., 1997, Mathematical Astronomy Morsels I, Willmann-Bell Inc., Richmond
- Morrison L.V., 1980, On the analysis of megalithic lunar sightlines in Scotland’, Archaeoastronomy, (in:) Supplement of the Journal for the History of Astronomy, 1980, 2: 65–77
- Rejis V., 2003, Investigating the major standstill limits in 2006
- Sampson R.D., 2000, Astronomical refraction and the equinox sunrise, Journal of the Royal Astronomical Society of Canada, Vol 94, pp. 26–29.
- Schaefer B.E., Liller W., 1990, Refraction near the horizon, (in:) Publications of the Astronomical Society of the
Pacific, Vol. 102, pp. 796–805. - Sédillot, L.P.E.A., 1853. Prolégomènes des tables astronomiques d’OlougBeg: Traduction et commentaire (in:) Paris: Firmin Didot Frères. pp. 87 & 253
- Sims, L., 2006, What is a lunar standstill? Problems of accuracy and
validity in ‘the Thom paradigm’’. Mediterranean Archaeology & Archaeometry,
Special Issue 6 (3) 157-163. - Sims L., 2016, What is a lunar standstill III, (in:) Documenta Praehistorica, 2016, Vol 43, p467
- Sims L., 2016, What is the minor standstill of the Moon?, (in:) Journal of Skyscape Archeology 1:3
- Sims L., 2019, What is a lunar standstill IV, (in:) Journal of Skyscape Archeology
- Spravigna A. C., About the locution ‘lunar standstill’ and the term ‘lunistice’, Politecnico di Torino
- Świątek K., Dziwota T., 2020, Measuring distance to the Moon by parallax, European Association for Astronomy Education
- Thom A., 1971, Megalithic lunar observatories, Clarendon Press, Oxford
- Vincent F., 2005, A major lunar standstill, (in:) Journal of the British Astronomical Association, 115,4
Links:
- https://www.chimneyrockco.org/puebloan-resources/lunar-standstill/
- Archeoastronomical computations of the major lunar standstill
- Prehistoric lunar calendar
- Mega-what.com: What is lunistice?
- Eclipse.gsfc.nasa.gov: Moon’s orbit explanation
- https://public.nrao.edu/ask/why-isnt-the-precession-of-the-lunar-nodes-uniform-with-time/
- Astropixels.com: Greatest Annual Lunar Standstills
- http://www.archaeocosmology.org/eng/moonperb.htm
- Archaeocosmology.org: Lunar orbit fluctuation computations between BC4000 and AD2500
- https://www.peterthestoryteller.co.uk/page22a.html
- https://sherrytowers.com/2014/04/12/some-handy-scripts-for-archeoastronomy/
- https://www.exploreglobe.net/major-lunar-standstill.html
- http://archaeocosmology.org/eng/moonperb.htm#Azimuth
- http://archaeocosmology.org/eng/moonthomas.htm
- https://www.umass.edu/sunwheel/pages/moonteaching.html
- Archaeocosmology.org: Major lunar standstill
- https://www.skyscript.co.uk/lss.html
- https://www.perseus.gr/Astro-Lunar-Scenes-Major-Standstill-2006.htm
- https://cohost.org/spiders/post/3113937-the-moon-is-not-norm
- https://www.mooncalc.org/
- https://www.english-heritage.org.uk/visit/places/stonehenge/things-to-do/major-lunar-standstill/
- https://www.theguardian.com/uk-news/2024/apr/15/once-in-a-generation-lunar-event-to-shed-light-on-stonehenges-links-to-the-moon
- Stonehenge research explores possible Moon connection
- https://www.heritagedaily.com/2024/04/moon-may-have-influenced-stonehenge-construction/151629
- https://www.futura-sciences.com/sciences/actualites/archeologie-astronomie-cet-evenement-exceptionnel-pourrait-eclairer-mysterieux-lien-stonehenge-lune-113053/ (French)
- https://blog.stonehenge-stone-circle.co.uk/2024/04/21/stonehenge-eclipse-of-the-moonmen/
- https://www.lunarsites-scotland.net/
- http://www.megalithicsites.co.uk/
- Aa.usno.navy.mil: Celestial Navigation Data for Assumed Position and Time
- Given the latitudes and longitudes of two places on earth, what is the (great circle) distance between them?
- https://oic-nwreviewer.blogspot.com/2014/05/find-true-azimuth-at-sunrise.html
- https://app.photoephemeris.com/
- https://www.space.com/moon-lunar-standstill-stonehenge-alignment
- https://infogalactic.com/info/Lunar_standstill
- https://everything.explained.today/Lunar_standstill/
- https://edition.cnn.com/2024/05/21/world/stonehenge-moon-lunar-standstill-scn/index.html
- https://phys.org/news/2024-04-stonehenge-aligned-moon-sun.html
- https://callanish.archaeoptics.co.uk/archaeoastronomy.html
Forums:
- https://www.reddit.com/r/askastronomy/comments/lyn14b/can_someone_explain_to_me_what_exactly_a_lunar/
- https://www.reddit.com/r/explainlikeimfive/comments/1s5s05/eli5_what_is_a_lunar_standstill/
- https://astronomy.stackexchange.com/questions/50935/how-do-times-of-lunar-standstills-vary-over-time-if-we-folded-them-back-into-a
- https://astronomy.stackexchange.com/questions/57296/is-the-moons-orbital-plane-angle-relative-to-the-ecliptic-constant
- https://www.cloudynights.com/topic/80065-end-of-the-major-lunar-standstill-season/
- https://astronomy.stackexchange.com/questions/47545/where-is-it-possible-to-observe-the-moon-for-24-hours
- Megalithic.co.uk: What is a lunar standstill?
- Megalithic.co.uk: Major lunar standstill south
- Cloudynights.com: 2024-2025 Major lunar standstill and standstill nodes till 2043
- https://astronomy.stackexchange.com/questions/43717/using-parallax-to-find-distance-to-the-moon
- https://www.reddit.com/r/worldbuilding/comments/11xlufn/a_formula_to_calculate_the_size_of_a_moon_in_the/
- https://astronomy.stackexchange.com/questions/7736/what-is-the-angular-diameter-of-earth-as-seen-from-the-moon
- https://astronomy.stackexchange.com/questions/240/how-does-moonrise-moonset-azimuth-vary-with-time
- https://astronomy.stackexchange.com/questions/57586/what-is-the-longest-time-the-moon-can-stay-in-the-sky/57591#57591
- https://astronomy.stackexchange.com/questions/28642/precise-declination-of-moon
- https://astronomy.stackexchange.com/questions/47502/how-to-calculate-the-nodal-precession-range-of-the-moon-with-respect-to-the-cele
My questions:
- https://astronomy.stackexchange.com/questions/57780/how-does-azimuth-of-moonrise-moonset-vary-by-longitude
- https://astronomy.stackexchange.com/questions/57680/calculating-lunar-parallax-based-on-a-distance-between-two-objects-at-certain-la
Wiki:
- Axial_tilt
- Ecliptic
- Exeligmos
- Lunar_node
- Metonic_cycle
- Nodal_precession
- Orbit_of_the_Moon
- Orbital_node
- Solar_azimuth_angle
- Stonehenge
Youtube: